Code for Workshop: Introduction to Machine Learning with R
These are the slides from my workshop: Introduction to Machine Learning with R which I gave at the University of Heidelberg, Germany on June 28th 2018. The entire code accompanying the workshop can be found below the video.
The workshop covered the basics of machine learning. With an example dataset I went through a standard machine learning workflow in R with the packages caret and h2o:
- reading in data
- exploratory data analysis
- missingness
- feature engineering
- training and test split
- model training with Random Forests, Gradient Boosting, Neural Nets, etc.
- hyperparameter tuning
Setup
All analyses are done in R using RStudio. For detailed session information including R version, operating system and package versions, see the sessionInfo() output at the end of this document.
All figures are produced with ggplot2.
- libraries
library(tidyverse) # for tidy data analysis
library(readr) # for fast reading of input files
library(mice) # mice package for Multivariate Imputation by Chained Equations (MICE)Data preparation
The dataset
The dataset I am using in these example analyses, is the Breast Cancer Wisconsin (Diagnostic) Dataset. The data was downloaded from the UC Irvine Machine Learning Repository.
The first dataset looks at the predictor classes:
- malignant or
- benign breast mass.
The features characterise cell nucleus properties and were generated from image analysis of fine needle aspirates (FNA) of breast masses:
- Sample ID (code number)
- Clump thickness
- Uniformity of cell size
- Uniformity of cell shape
- Marginal adhesion
- Single epithelial cell size
- Number of bare nuclei
- Bland chromatin
- Number of normal nuclei
- Mitosis
- Classes, i.e. diagnosis
bc_data <- read_delim("datasets/breast-cancer-wisconsin.data.txt",
delim = ",",
col_names = c("sample_code_number",
"clump_thickness",
"uniformity_of_cell_size",
"uniformity_of_cell_shape",
"marginal_adhesion",
"single_epithelial_cell_size",
"bare_nuclei",
"bland_chromatin",
"normal_nucleoli",
"mitosis",
"classes")) %>%
mutate(bare_nuclei = as.numeric(bare_nuclei),
classes = ifelse(classes == "2", "benign",
ifelse(classes == "4", "malignant", NA)))summary(bc_data)## sample_code_number clump_thickness uniformity_of_cell_size
## Min. : 61634 Min. : 1.000 Min. : 1.000
## 1st Qu.: 870688 1st Qu.: 2.000 1st Qu.: 1.000
## Median : 1171710 Median : 4.000 Median : 1.000
## Mean : 1071704 Mean : 4.418 Mean : 3.134
## 3rd Qu.: 1238298 3rd Qu.: 6.000 3rd Qu.: 5.000
## Max. :13454352 Max. :10.000 Max. :10.000
##
## uniformity_of_cell_shape marginal_adhesion single_epithelial_cell_size
## Min. : 1.000 Min. : 1.000 Min. : 1.000
## 1st Qu.: 1.000 1st Qu.: 1.000 1st Qu.: 2.000
## Median : 1.000 Median : 1.000 Median : 2.000
## Mean : 3.207 Mean : 2.807 Mean : 3.216
## 3rd Qu.: 5.000 3rd Qu.: 4.000 3rd Qu.: 4.000
## Max. :10.000 Max. :10.000 Max. :10.000
##
## bare_nuclei bland_chromatin normal_nucleoli mitosis
## Min. : 1.000 Min. : 1.000 Min. : 1.000 Min. : 1.000
## 1st Qu.: 1.000 1st Qu.: 2.000 1st Qu.: 1.000 1st Qu.: 1.000
## Median : 1.000 Median : 3.000 Median : 1.000 Median : 1.000
## Mean : 3.545 Mean : 3.438 Mean : 2.867 Mean : 1.589
## 3rd Qu.: 6.000 3rd Qu.: 5.000 3rd Qu.: 4.000 3rd Qu.: 1.000
## Max. :10.000 Max. :10.000 Max. :10.000 Max. :10.000
## NA's :16
## classes
## Length:699
## Class :character
## Mode :character
##
##
##
## Missing data
# how many NAs are in the data
md.pattern(bc_data, plot = FALSE)## sample_code_number clump_thickness uniformity_of_cell_size
## 683 1 1 1
## 16 1 1 1
## 0 0 0
## uniformity_of_cell_shape marginal_adhesion single_epithelial_cell_size
## 683 1 1 1
## 16 1 1 1
## 0 0 0
## bland_chromatin normal_nucleoli mitosis classes bare_nuclei
## 683 1 1 1 1 1 0
## 16 1 1 1 1 0 1
## 0 0 0 0 16 16bc_data <- bc_data %>%
drop_na() %>%
select(classes, everything(), -sample_code_number)
head(bc_data)## # A tibble: 6 x 10
## classes clump_thickness uniformity_of_cell_si… uniformity_of_cell_sha…
## <chr> <int> <int> <int>
## 1 benign 5 1 1
## 2 benign 5 4 4
## 3 benign 3 1 1
## 4 benign 6 8 8
## 5 benign 4 1 1
## 6 malignant 8 10 10
## # ... with 6 more variables: marginal_adhesion <int>,
## # single_epithelial_cell_size <int>, bare_nuclei <dbl>,
## # bland_chromatin <int>, normal_nucleoli <int>, mitosis <int>Missing values can be imputed with the mice package.
More info and tutorial with code: https://shirinsplayground.netlify.com/2018/04/flu_prediction/
Data exploration
- Response variable for classification
ggplot(bc_data, aes(x = classes, fill = classes)) +
geom_bar()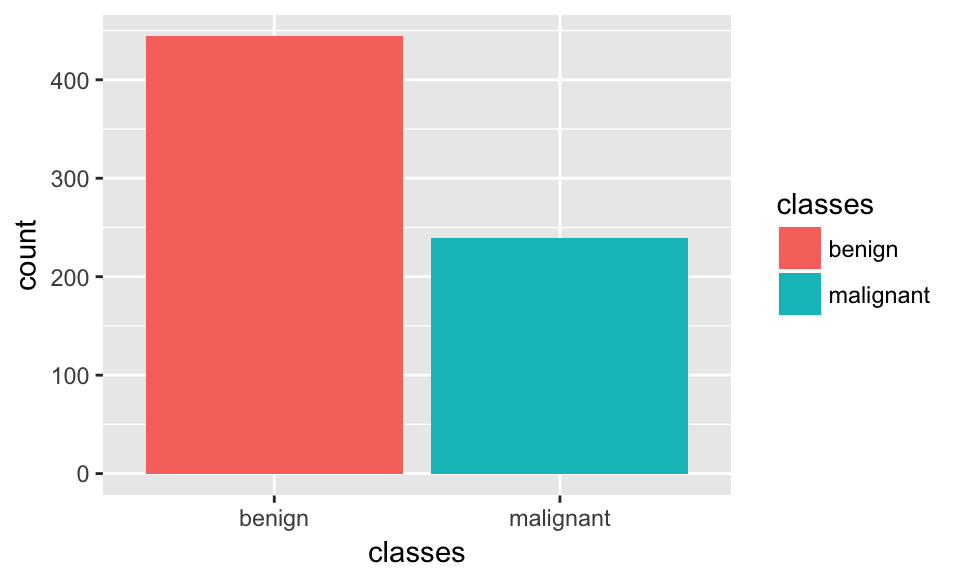
More info on dealing with unbalanced classes: https://shiring.github.io/machine_learning/2017/04/02/unbalanced
- Response variable for regression
ggplot(bc_data, aes(x = clump_thickness)) +
geom_histogram(bins = 10)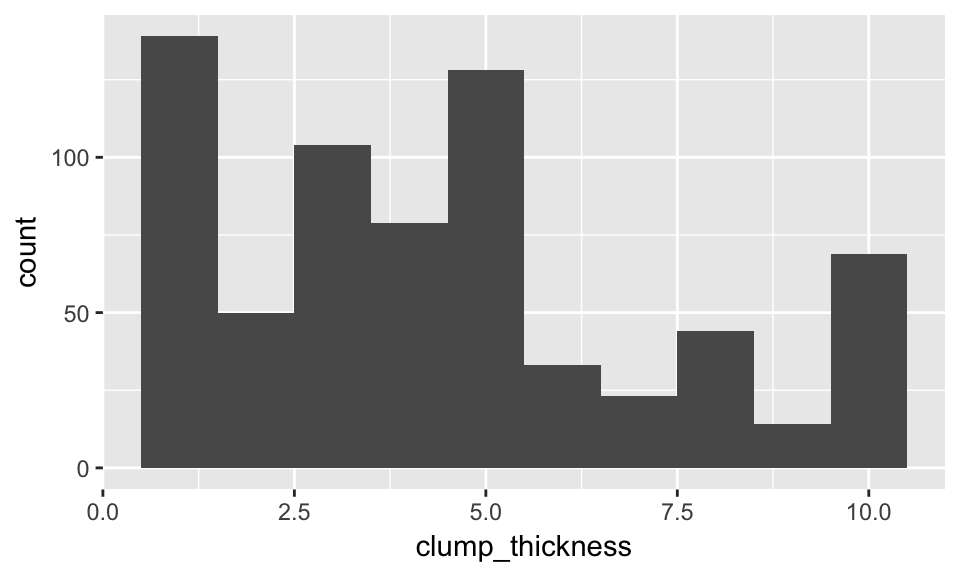
- Features
gather(bc_data, x, y, clump_thickness:mitosis) %>%
ggplot(aes(x = y, color = classes, fill = classes)) +
geom_density(alpha = 0.3) +
facet_wrap( ~ x, scales = "free", ncol = 3)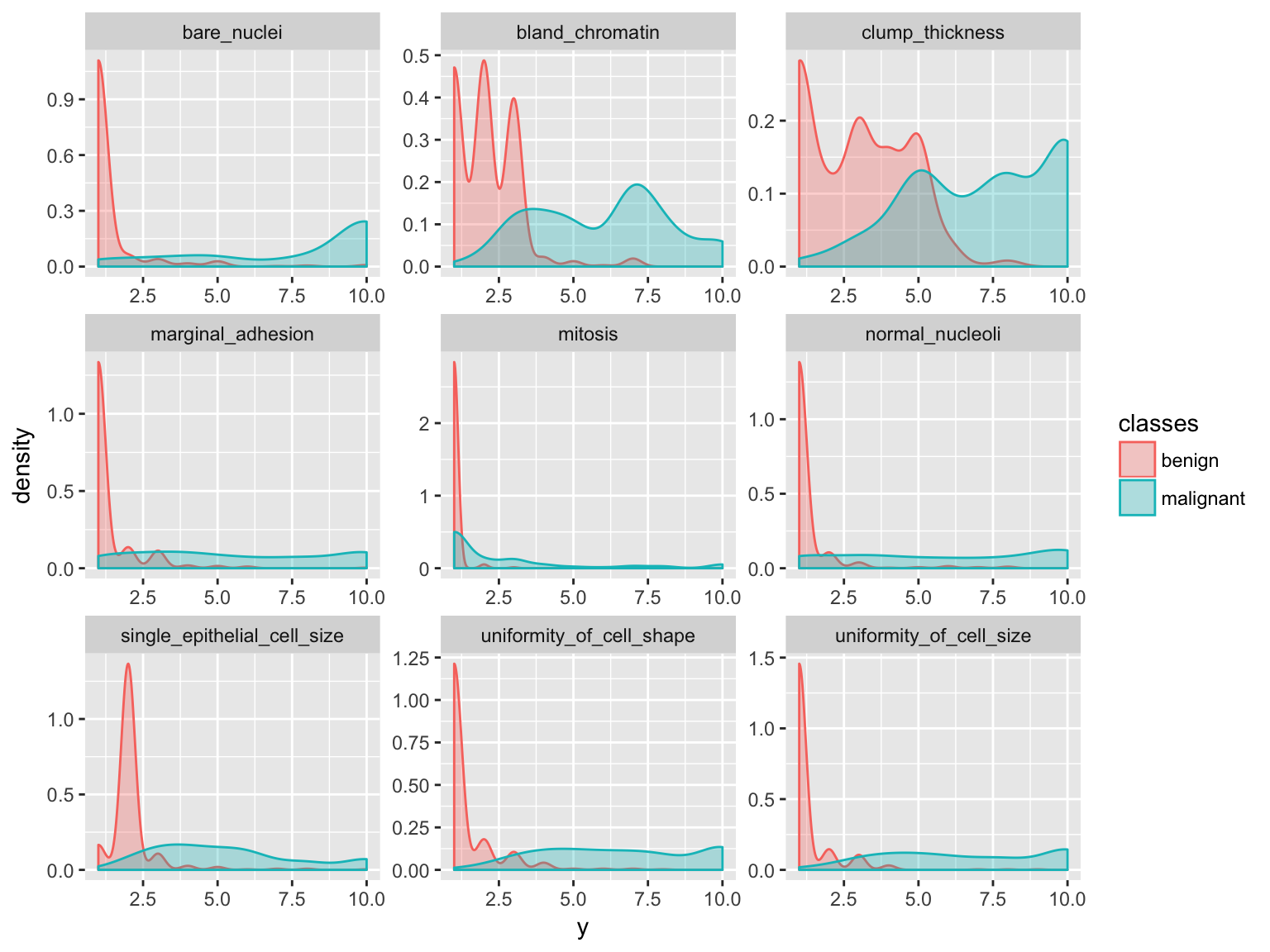
- Correlation graphs
co_mat_benign <- filter(bc_data, classes == "benign") %>%
select(-1) %>%
cor()
co_mat_malignant <- filter(bc_data, classes == "malignant") %>%
select(-1) %>%
cor()
library(igraph)
g_benign <- graph.adjacency(co_mat_benign,
weighted = TRUE,
diag = FALSE,
mode = "upper")
g_malignant <- graph.adjacency(co_mat_malignant,
weighted = TRUE,
diag = FALSE,
mode = "upper")
# http://kateto.net/networks-r-igraph
cut.off_b <- mean(E(g_benign)$weight)
cut.off_m <- mean(E(g_malignant)$weight)
g_benign_2 <- delete_edges(g_benign, E(g_benign)[weight < cut.off_b])
g_malignant_2 <- delete_edges(g_malignant, E(g_malignant)[weight < cut.off_m])
c_g_benign_2 <- cluster_fast_greedy(g_benign_2)
c_g_malignant_2 <- cluster_fast_greedy(g_malignant_2) par(mfrow = c(1,2))
plot(c_g_benign_2, g_benign_2,
vertex.size = colSums(co_mat_benign) * 10,
vertex.frame.color = NA,
vertex.label.color = "black",
vertex.label.cex = 0.8,
edge.width = E(g_benign_2)$weight * 15,
layout = layout_with_fr(g_benign_2),
main = "Benign tumors")
plot(c_g_malignant_2, g_malignant_2,
vertex.size = colSums(co_mat_malignant) * 10,
vertex.frame.color = NA,
vertex.label.color = "black",
vertex.label.cex = 0.8,
edge.width = E(g_malignant_2)$weight * 15,
layout = layout_with_fr(g_malignant_2),
main = "Malignant tumors")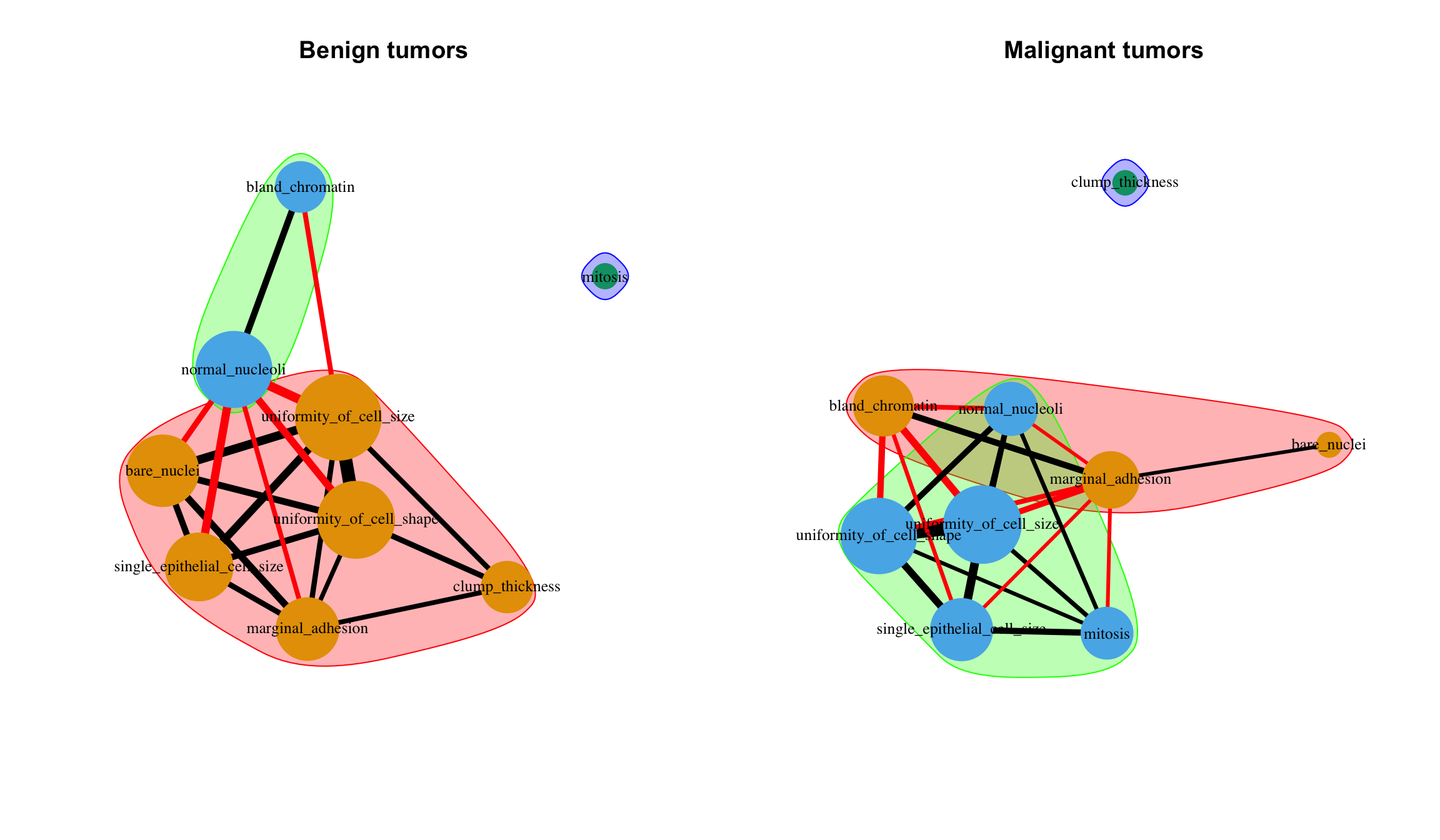
Principal Component Analysis
library(ellipse)
# perform pca and extract scores
pcaOutput <- prcomp(as.matrix(bc_data[, -1]), scale = TRUE, center = TRUE)
pcaOutput2 <- as.data.frame(pcaOutput$x)
# define groups for plotting
pcaOutput2$groups <- bc_data$classes
centroids <- aggregate(cbind(PC1, PC2) ~ groups, pcaOutput2, mean)
conf.rgn <- do.call(rbind, lapply(unique(pcaOutput2$groups), function(t)
data.frame(groups = as.character(t),
ellipse(cov(pcaOutput2[pcaOutput2$groups == t, 1:2]),
centre = as.matrix(centroids[centroids$groups == t, 2:3]),
level = 0.95),
stringsAsFactors = FALSE)))
ggplot(data = pcaOutput2, aes(x = PC1, y = PC2, group = groups, color = groups)) +
geom_polygon(data = conf.rgn, aes(fill = groups), alpha = 0.2) +
geom_point(size = 2, alpha = 0.6) +
labs(color = "",
fill = "") 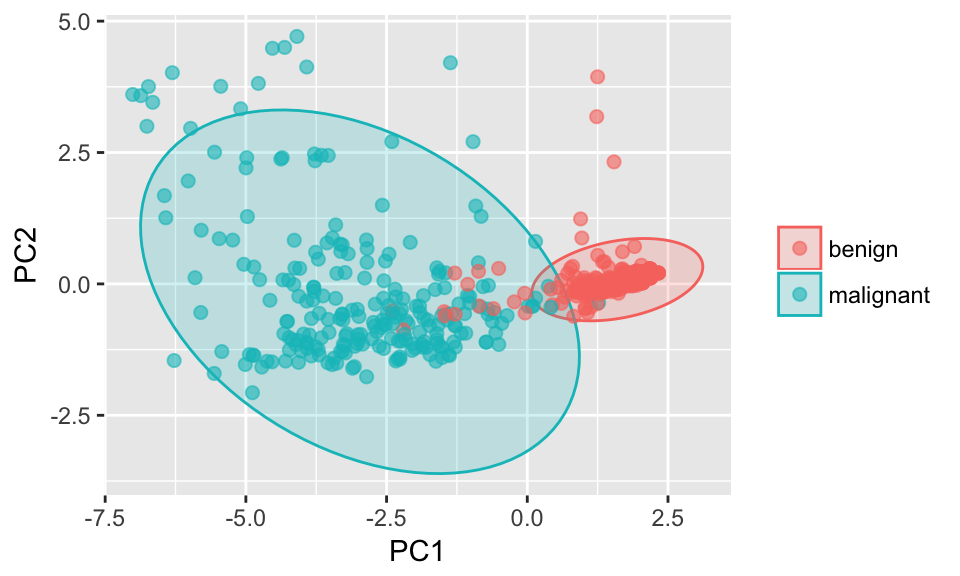
Multidimensional Scaling
select(bc_data, -1) %>%
dist() %>%
cmdscale %>%
as.data.frame() %>%
mutate(group = bc_data$classes) %>%
ggplot(aes(x = V1, y = V2, color = group)) +
geom_point()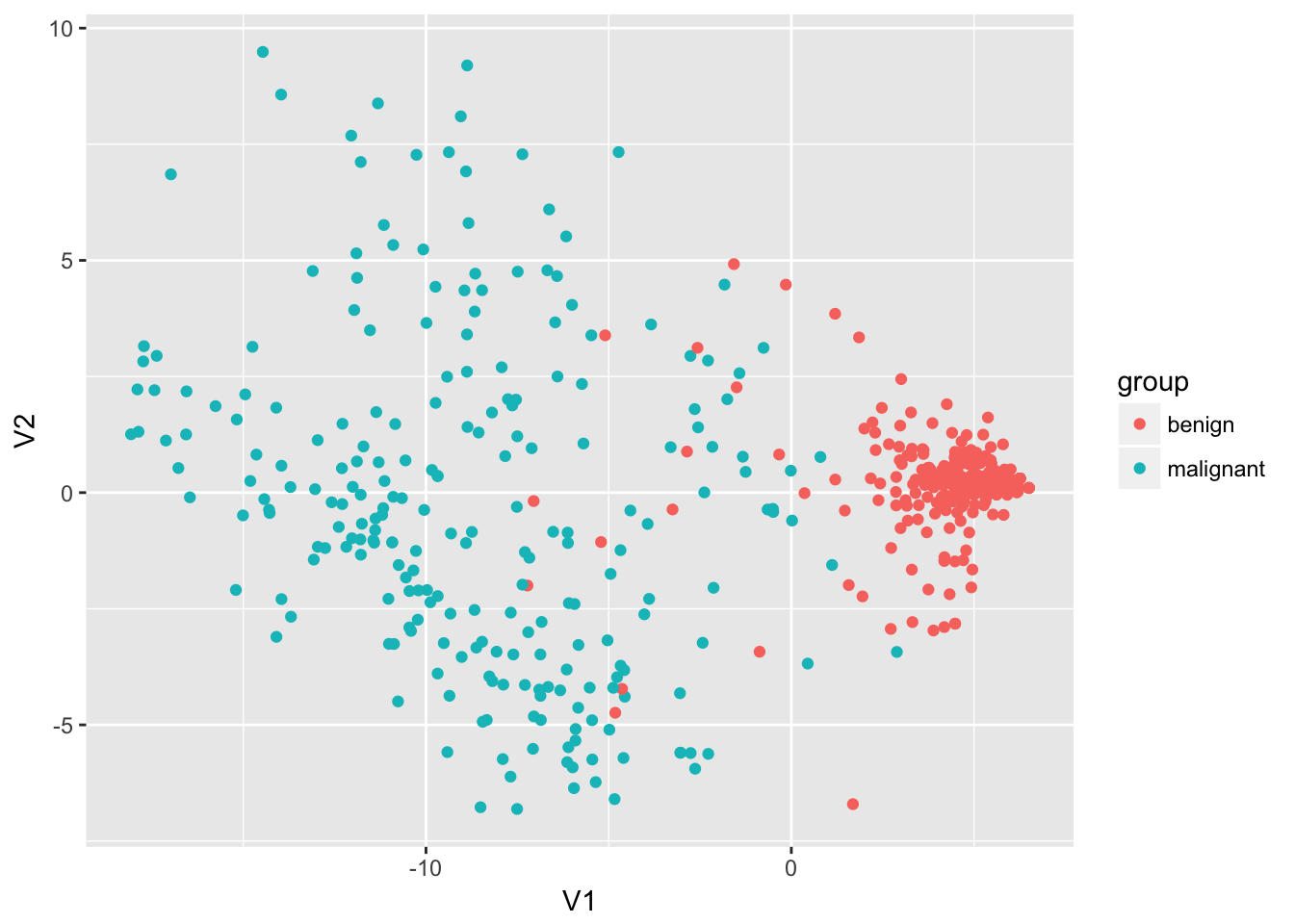
t-SNE dimensionality reduction
library(tsne)
select(bc_data, -1) %>%
dist() %>%
tsne() %>%
as.data.frame() %>%
mutate(group = bc_data$classes) %>%
ggplot(aes(x = V1, y = V2, color = group)) +
geom_point()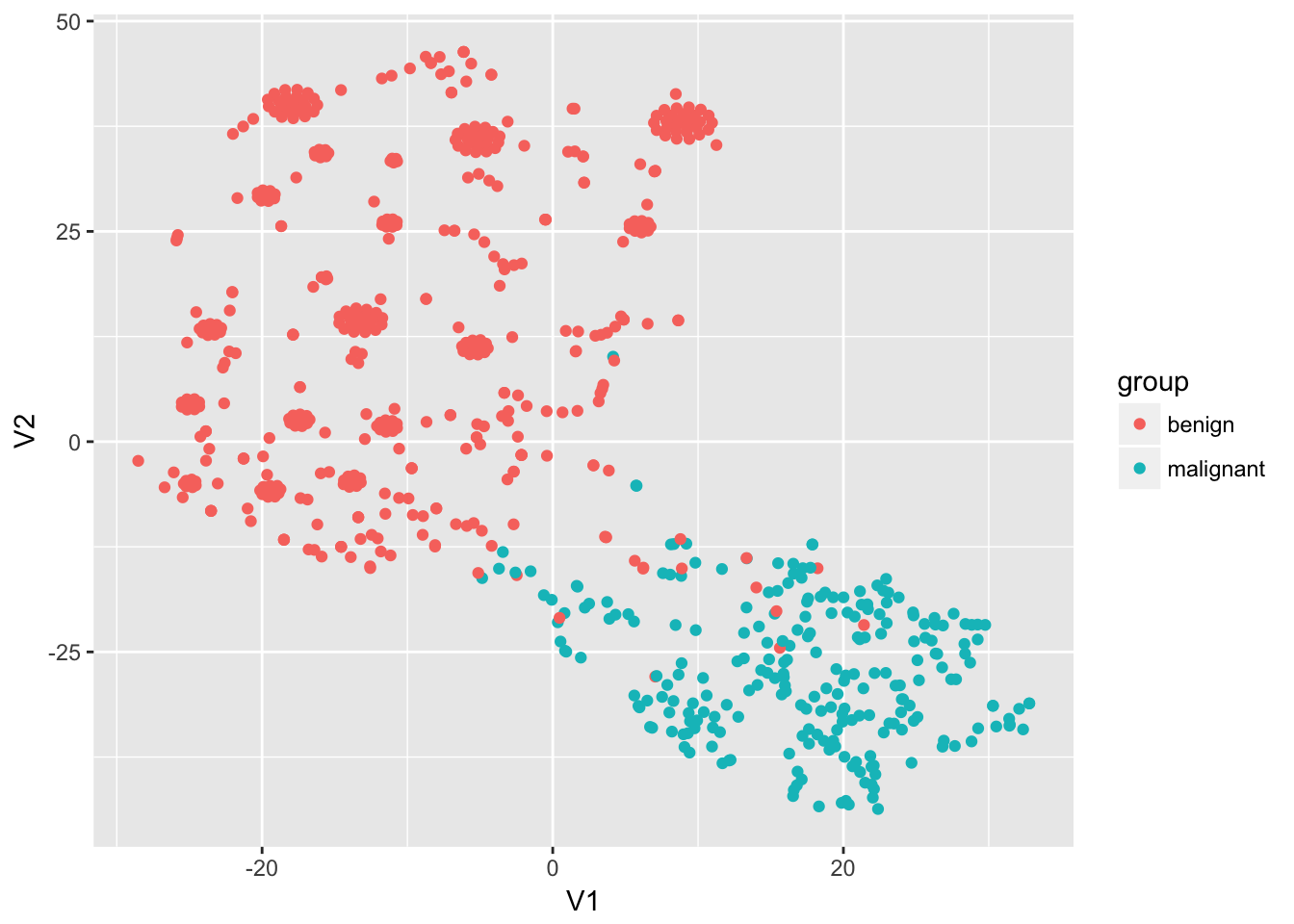
Machine Learning packages for R
caret
# configure multicore
library(doParallel)
cl <- makeCluster(detectCores())
registerDoParallel(cl)
library(caret)Training, validation and test data
set.seed(42)
index <- createDataPartition(bc_data$classes, p = 0.7, list = FALSE)
train_data <- bc_data[index, ]
test_data <- bc_data[-index, ]bind_rows(data.frame(group = "train", train_data),
data.frame(group = "test", test_data)) %>%
gather(x, y, clump_thickness:mitosis) %>%
ggplot(aes(x = y, color = group, fill = group)) +
geom_density(alpha = 0.3) +
facet_wrap( ~ x, scales = "free", ncol = 3)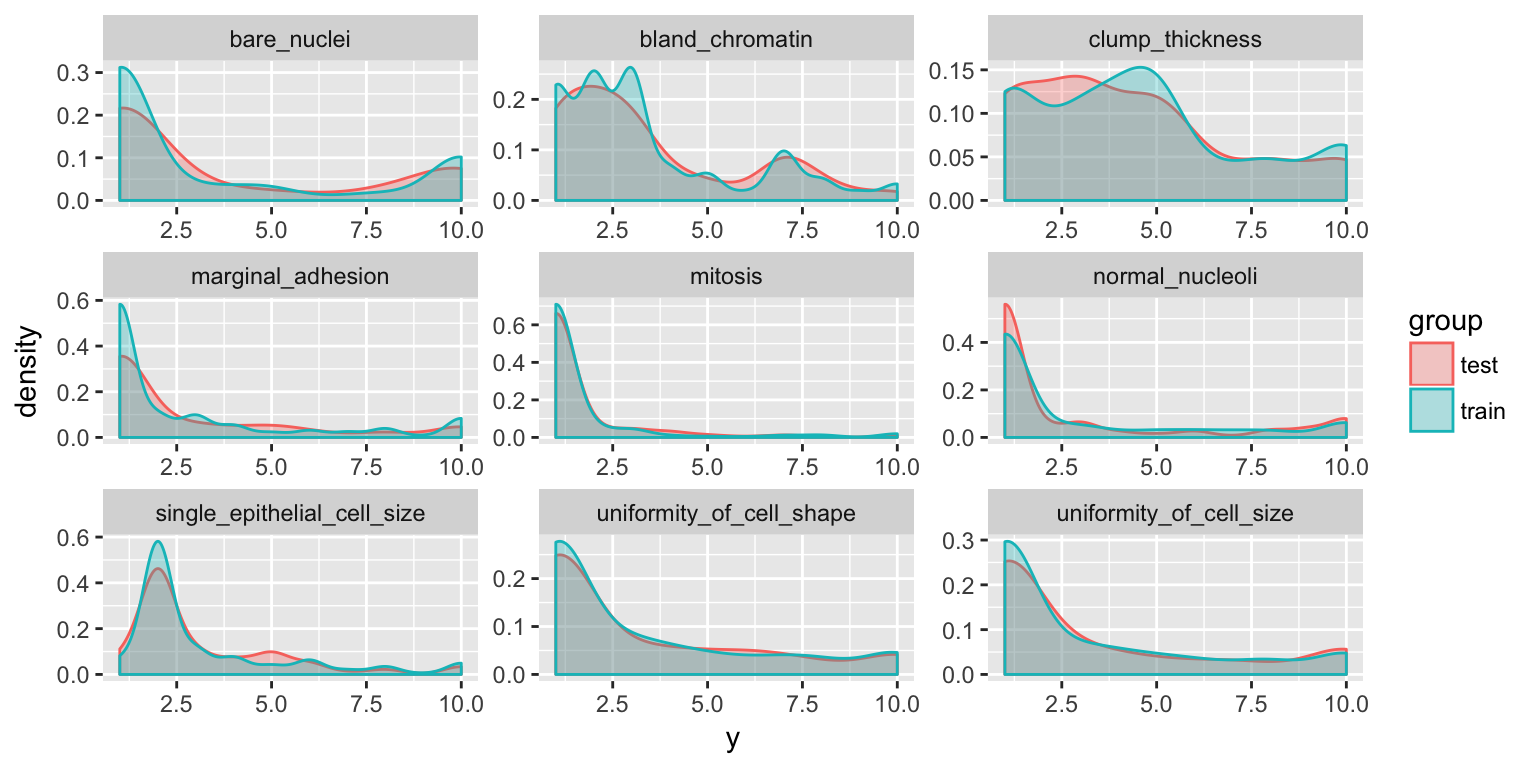
Regression
set.seed(42)
model_glm <- caret::train(clump_thickness ~ .,
data = train_data,
method = "glm",
preProcess = c("scale", "center"),
trControl = trainControl(method = "repeatedcv",
number = 10,
repeats = 10,
savePredictions = TRUE,
verboseIter = FALSE))model_glm## Generalized Linear Model
##
## 479 samples
## 9 predictor
##
## Pre-processing: scaled (9), centered (9)
## Resampling: Cross-Validated (10 fold, repeated 10 times)
## Summary of sample sizes: 432, 431, 432, 431, 431, 431, ...
## Resampling results:
##
## RMSE Rsquared MAE
## 1.972314 0.5254215 1.648832predictions <- predict(model_glm, test_data)# model_glm$finalModel$linear.predictors == model_glm$finalModel$fitted.values
data.frame(residuals = resid(model_glm),
predictors = model_glm$finalModel$linear.predictors) %>%
ggplot(aes(x = predictors, y = residuals)) +
geom_jitter() +
geom_smooth(method = "lm")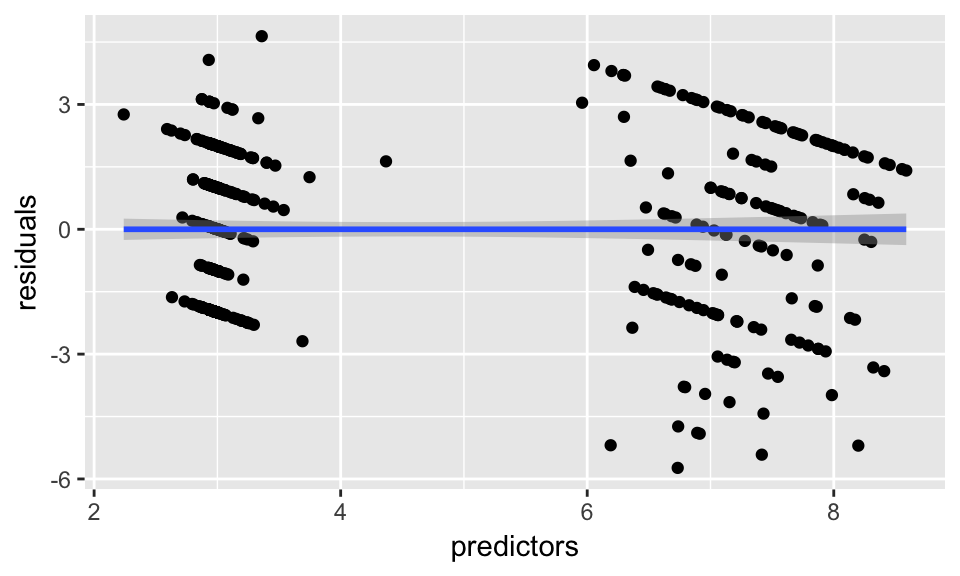
# y == train_data$clump_thickness
data.frame(residuals = resid(model_glm),
y = model_glm$finalModel$y) %>%
ggplot(aes(x = y, y = residuals)) +
geom_jitter() +
geom_smooth(method = "lm")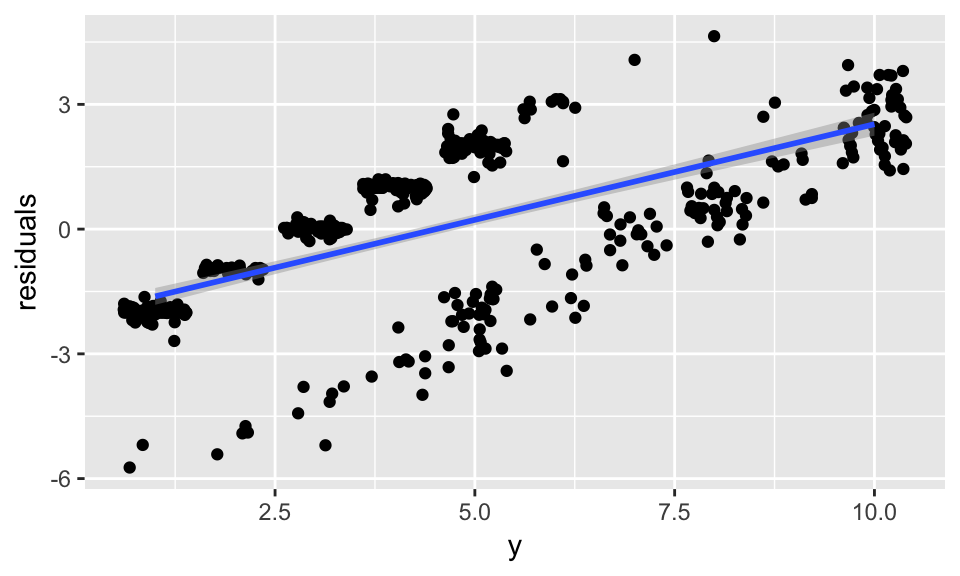
data.frame(actual = test_data$clump_thickness,
predicted = predictions) %>%
ggplot(aes(x = actual, y = predicted)) +
geom_jitter() +
geom_smooth(method = "lm")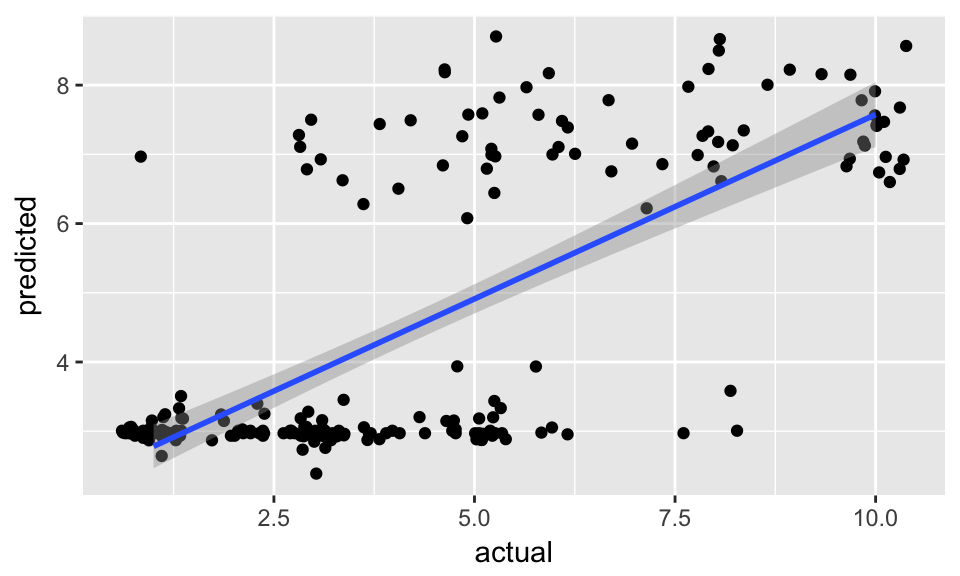
Classification
Decision trees
library(rpart)
library(rpart.plot)
set.seed(42)
fit <- rpart(classes ~ .,
data = train_data,
method = "class",
control = rpart.control(xval = 10,
minbucket = 2,
cp = 0),
parms = list(split = "information"))
rpart.plot(fit, extra = 100)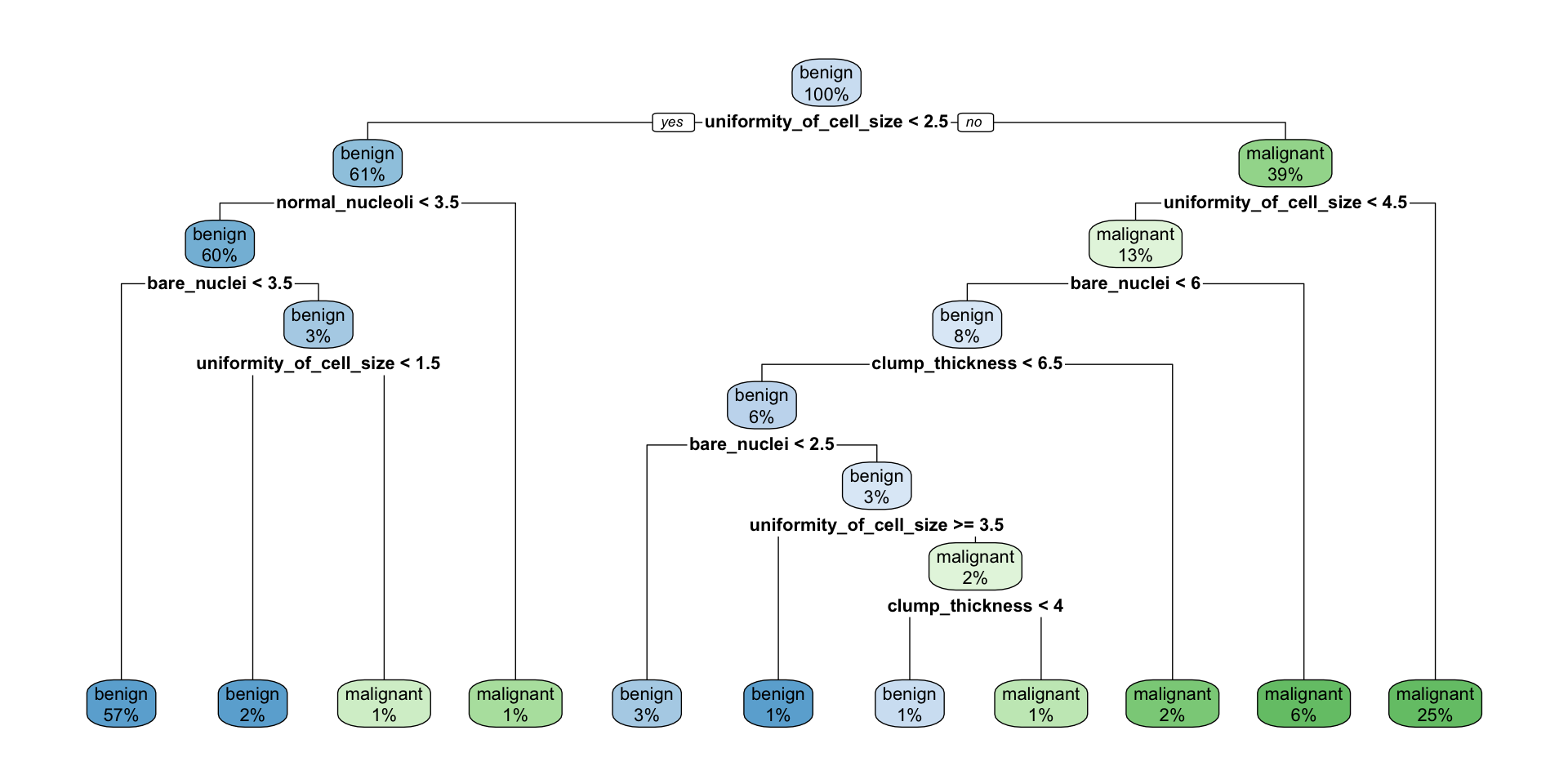
Random Forests
Random Forests predictions are based on the generation of multiple classification trees. They can be used for both, classification and regression tasks. Here, I show a classification task.
set.seed(42)
model_rf <- caret::train(classes ~ .,
data = train_data,
method = "rf",
preProcess = c("scale", "center"),
trControl = trainControl(method = "repeatedcv",
number = 5,
repeats = 3,
savePredictions = TRUE,
verboseIter = FALSE))When you specify savePredictions = TRUE, you can access the cross-validation resuls with model_rf$pred.
model_rf## Random Forest
##
## 479 samples
## 9 predictor
## 2 classes: 'benign', 'malignant'
##
## Pre-processing: scaled (9), centered (9)
## Resampling: Cross-Validated (10 fold, repeated 10 times)
## Summary of sample sizes: 432, 431, 431, 431, 431, 431, ...
## Resampling results across tuning parameters:
##
## mtry Accuracy Kappa
## 2 0.9776753 0.9513499
## 5 0.9757957 0.9469999
## 9 0.9714200 0.9370285
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 2.model_rf$finalModel$confusion## benign malignant class.error
## benign 304 7 0.02250804
## malignant 5 163 0.02976190Dealing with unbalanced data
Luckily, caret makes it very easy to incorporate over- and under-sampling techniques with cross-validation resampling. We can simply add the sampling option to our trainControl and choose down for under- (also called down-) sampling. The rest stays the same as with our original model.
set.seed(42)
model_rf_down <- caret::train(classes ~ .,
data = train_data,
method = "rf",
preProcess = c("scale", "center"),
trControl = trainControl(method = "repeatedcv",
number = 10,
repeats = 10,
savePredictions = TRUE,
verboseIter = FALSE,
sampling = "down"))model_rf_down## Random Forest
##
## 479 samples
## 9 predictor
## 2 classes: 'benign', 'malignant'
##
## Pre-processing: scaled (9), centered (9)
## Resampling: Cross-Validated (10 fold, repeated 10 times)
## Summary of sample sizes: 432, 431, 431, 431, 431, 431, ...
## Addtional sampling using down-sampling prior to pre-processing
##
## Resampling results across tuning parameters:
##
## mtry Accuracy Kappa
## 2 0.9797503 0.9563138
## 5 0.9741198 0.9438326
## 9 0.9699578 0.9346310
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 2.Feature Importance
imp <- model_rf$finalModel$importance
imp[order(imp, decreasing = TRUE), ]## uniformity_of_cell_size uniformity_of_cell_shape
## 43.936945 39.840595
## bare_nuclei bland_chromatin
## 33.820345 31.984813
## normal_nucleoli single_epithelial_cell_size
## 21.686039 17.761202
## clump_thickness marginal_adhesion
## 16.318817 9.518437
## mitosis
## 2.220633# estimate variable importance
importance <- varImp(model_rf, scale = TRUE)
plot(importance)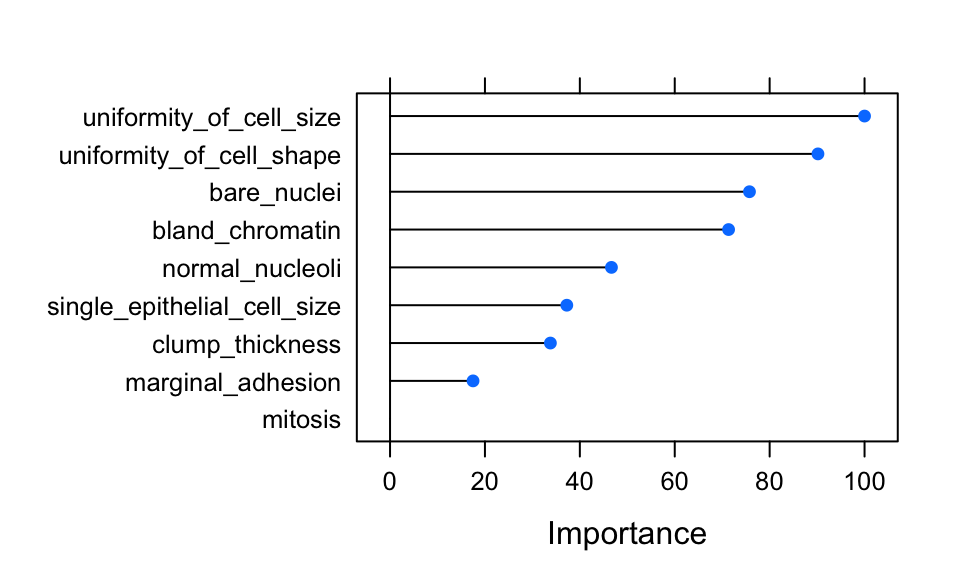
- predicting test data
confusionMatrix(predict(model_rf, test_data), as.factor(test_data$classes))## Confusion Matrix and Statistics
##
## Reference
## Prediction benign malignant
## benign 128 4
## malignant 5 67
##
## Accuracy : 0.9559
## 95% CI : (0.9179, 0.9796)
## No Information Rate : 0.652
## P-Value [Acc > NIR] : <2e-16
##
## Kappa : 0.9031
## Mcnemar's Test P-Value : 1
##
## Sensitivity : 0.9624
## Specificity : 0.9437
## Pos Pred Value : 0.9697
## Neg Pred Value : 0.9306
## Prevalence : 0.6520
## Detection Rate : 0.6275
## Detection Prevalence : 0.6471
## Balanced Accuracy : 0.9530
##
## 'Positive' Class : benign
## results <- data.frame(actual = test_data$classes,
predict(model_rf, test_data, type = "prob"))
results$prediction <- ifelse(results$benign > 0.5, "benign",
ifelse(results$malignant > 0.5, "malignant", NA))
results$correct <- ifelse(results$actual == results$prediction, TRUE, FALSE)
ggplot(results, aes(x = prediction, fill = correct)) +
geom_bar(position = "dodge")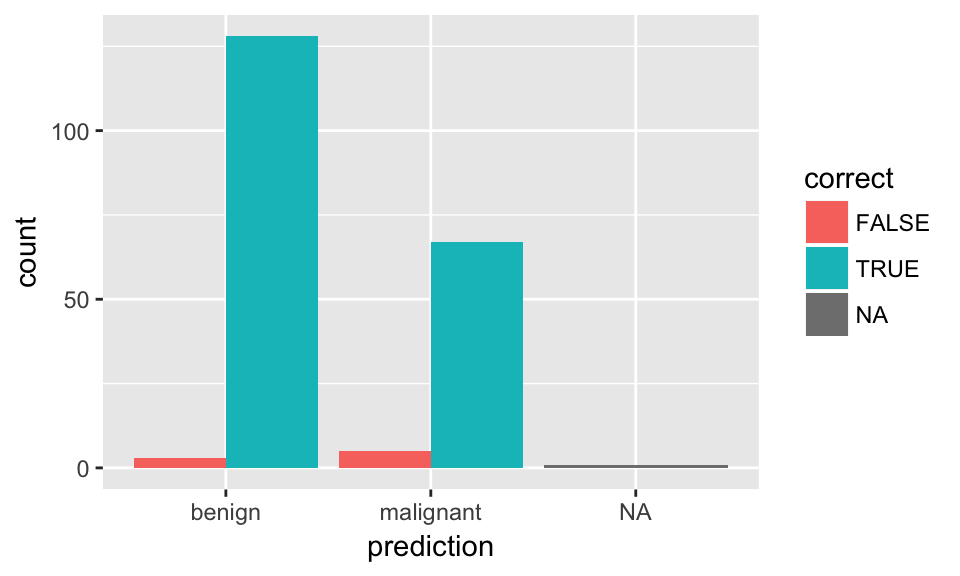
ggplot(results, aes(x = prediction, y = benign, color = correct, shape = correct)) +
geom_jitter(size = 3, alpha = 0.6)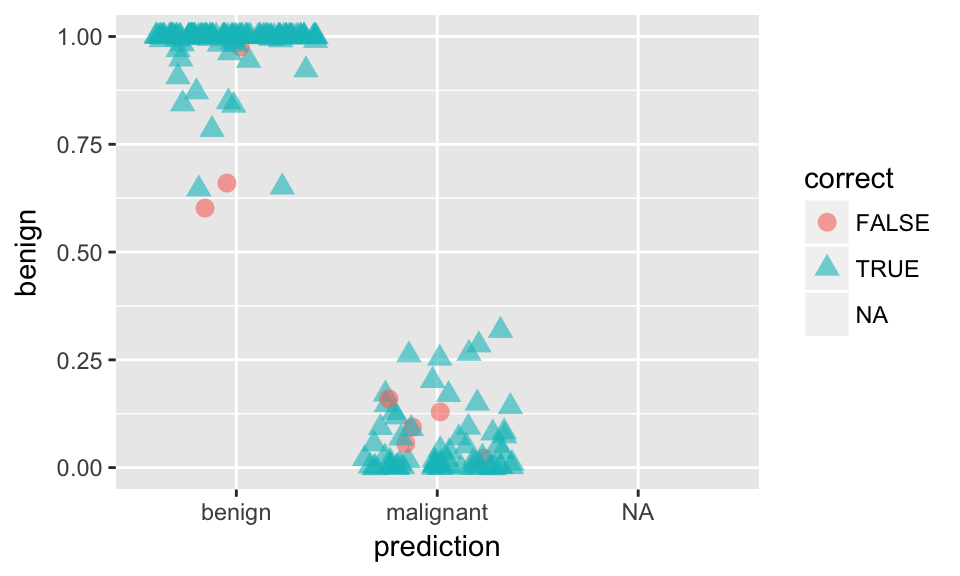
Extreme gradient boosting trees
Extreme gradient boosting (XGBoost) is a faster and improved implementation of gradient boosting for supervised learning.
“XGBoost uses a more regularized model formalization to control over-fitting, which gives it better performance.” Tianqi Chen, developer of xgboost
XGBoost is a tree ensemble model, which means the sum of predictions from a set of classification and regression trees (CART). In that, XGBoost is similar to Random Forests but it uses a different approach to model training. Can be used for classification and regression tasks. Here, I show a classification task.
set.seed(42)
model_xgb <- caret::train(classes ~ .,
data = train_data,
method = "xgbTree",
preProcess = c("scale", "center"),
trControl = trainControl(method = "repeatedcv",
number = 5,
repeats = 3,
savePredictions = TRUE,
verboseIter = FALSE))model_xgb## eXtreme Gradient Boosting
##
## 479 samples
## 9 predictor
## 2 classes: 'benign', 'malignant'
##
## Pre-processing: scaled (9), centered (9)
## Resampling: Cross-Validated (10 fold, repeated 10 times)
## Summary of sample sizes: 432, 431, 431, 431, 431, 431, ...
## Resampling results across tuning parameters:
##
## eta max_depth colsample_bytree subsample nrounds Accuracy
## 0.3 1 0.6 0.50 50 0.9567788
## 0.3 1 0.6 0.50 100 0.9544912
## 0.3 1 0.6 0.50 150 0.9513572
## 0.3 1 0.6 0.75 50 0.9576164
## 0.3 1 0.6 0.75 100 0.9536448
## 0.3 1 0.6 0.75 150 0.9525987
## 0.3 1 0.6 1.00 50 0.9559409
## 0.3 1 0.6 1.00 100 0.9555242
## 0.3 1 0.6 1.00 150 0.9551031
## 0.3 1 0.8 0.50 50 0.9718588
## 0.3 1 0.8 0.50 100 0.9720583
## 0.3 1 0.8 0.50 150 0.9699879
## 0.3 1 0.8 0.75 50 0.9726964
## 0.3 1 0.8 0.75 100 0.9724664
## 0.3 1 0.8 0.75 150 0.9705868
## 0.3 1 0.8 1.00 50 0.9714202
## 0.3 1 0.8 1.00 100 0.9710035
## 0.3 1 0.8 1.00 150 0.9705866
## 0.3 2 0.6 0.50 50 0.9559448
## 0.3 2 0.6 0.50 100 0.9565397
## 0.3 2 0.6 0.50 150 0.9555063
## 0.3 2 0.6 0.75 50 0.9530150
## 0.3 2 0.6 0.75 100 0.9550985
## 0.3 2 0.6 0.75 150 0.9551070
## 0.3 2 0.6 1.00 50 0.9532320
## 0.3 2 0.6 1.00 100 0.9551072
## 0.3 2 0.6 1.00 150 0.9557237
## 0.3 2 0.8 0.50 50 0.9720583
## 0.3 2 0.8 0.50 100 0.9735166
## 0.3 2 0.8 0.50 150 0.9720540
## 0.3 2 0.8 0.75 50 0.9722494
## 0.3 2 0.8 0.75 100 0.9726703
## 0.3 2 0.8 0.75 150 0.9716374
## 0.3 2 0.8 1.00 50 0.9716327
## 0.3 2 0.8 1.00 100 0.9724622
## 0.3 2 0.8 1.00 150 0.9718416
## 0.3 3 0.6 0.50 50 0.9548905
## 0.3 3 0.6 0.50 100 0.9557237
## 0.3 3 0.6 0.50 150 0.9555198
## 0.3 3 0.6 0.75 50 0.9561404
## 0.3 3 0.6 0.75 100 0.9546820
## 0.3 3 0.6 0.75 150 0.9552982
## 0.3 3 0.6 1.00 50 0.9577983
## 0.3 3 0.6 1.00 100 0.9573819
## 0.3 3 0.6 1.00 150 0.9567655
## 0.3 3 0.8 0.50 50 0.9733131
## 0.3 3 0.8 0.50 100 0.9728829
## 0.3 3 0.8 0.50 150 0.9718499
## 0.3 3 0.8 0.75 50 0.9751879
## 0.3 3 0.8 0.75 100 0.9743546
## 0.3 3 0.8 0.75 150 0.9735212
## 0.3 3 0.8 1.00 50 0.9743372
## 0.3 3 0.8 1.00 100 0.9737122
## 0.3 3 0.8 1.00 150 0.9743461
## 0.4 1 0.6 0.50 50 0.9548861
## 0.4 1 0.6 0.50 100 0.9528290
## 0.4 1 0.6 0.50 150 0.9498772
## 0.4 1 0.6 0.75 50 0.9557239
## 0.4 1 0.6 0.75 100 0.9513529
## 0.4 1 0.6 0.75 150 0.9492779
## 0.4 1 0.6 1.00 50 0.9559365
## 0.4 1 0.6 1.00 100 0.9551031
## 0.4 1 0.6 1.00 150 0.9536361
## 0.4 1 0.8 0.50 50 0.9710164
## 0.4 1 0.8 0.50 100 0.9697577
## 0.4 1 0.8 0.50 150 0.9687074
## 0.4 1 0.8 0.75 50 0.9710122
## 0.4 1 0.8 0.75 100 0.9707996
## 0.4 1 0.8 0.75 150 0.9691455
## 0.4 1 0.8 1.00 50 0.9705911
## 0.4 1 0.8 1.00 100 0.9697446
## 0.4 1 0.8 1.00 150 0.9697576
## 0.4 2 0.6 0.50 50 0.9544866
## 0.4 2 0.6 0.50 100 0.9542694
## 0.4 2 0.6 0.50 150 0.9536357
## 0.4 2 0.6 0.75 50 0.9540611
## 0.4 2 0.6 0.75 100 0.9542694
## 0.4 2 0.6 0.75 150 0.9549033
## 0.4 2 0.6 1.00 50 0.9540653
## 0.4 2 0.6 1.00 100 0.9555239
## 0.4 2 0.6 1.00 150 0.9546818
## 0.4 2 0.8 0.50 50 0.9720670
## 0.4 2 0.8 0.50 100 0.9695629
## 0.4 2 0.8 0.50 150 0.9702006
## 0.4 2 0.8 0.75 50 0.9722627
## 0.4 2 0.8 0.75 100 0.9720500
## 0.4 2 0.8 0.75 150 0.9716289
## 0.4 2 0.8 1.00 50 0.9726705
## 0.4 2 0.8 1.00 100 0.9708042
## 0.4 2 0.8 1.00 150 0.9708129
## 0.4 3 0.6 0.50 50 0.9555150
## 0.4 3 0.6 0.50 100 0.9553021
## 0.4 3 0.6 0.50 150 0.9548943
## 0.4 3 0.6 0.75 50 0.9555281
## 0.4 3 0.6 0.75 100 0.9563662
## 0.4 3 0.6 0.75 150 0.9555324
## 0.4 3 0.6 1.00 50 0.9575900
## 0.4 3 0.6 1.00 100 0.9571735
## 0.4 3 0.6 1.00 150 0.9559104
## 0.4 3 0.8 0.50 50 0.9737255
## 0.4 3 0.8 0.50 100 0.9745501
## 0.4 3 0.8 0.50 150 0.9730874
## 0.4 3 0.8 0.75 50 0.9747539
## 0.4 3 0.8 0.75 100 0.9724664
## 0.4 3 0.8 0.75 150 0.9720498
## 0.4 3 0.8 1.00 50 0.9747539
## 0.4 3 0.8 1.00 100 0.9749624
## 0.4 3 0.8 1.00 150 0.9734996
## Kappa
## 0.9050828
## 0.8999999
## 0.8930637
## 0.9067208
## 0.8982284
## 0.8959903
## 0.9028825
## 0.9022543
## 0.9014018
## 0.9382467
## 0.9386326
## 0.9340573
## 0.9400323
## 0.9395968
## 0.9353783
## 0.9372262
## 0.9362148
## 0.9353247
## 0.9032270
## 0.9047203
## 0.9024465
## 0.8968511
## 0.9015282
## 0.9016169
## 0.8971329
## 0.9015111
## 0.9028614
## 0.9387022
## 0.9419143
## 0.9387792
## 0.9391933
## 0.9401872
## 0.9379714
## 0.9377309
## 0.9397601
## 0.9384827
## 0.9008861
## 0.9029797
## 0.9024531
## 0.9037859
## 0.9004226
## 0.9019909
## 0.9074584
## 0.9064701
## 0.9051441
## 0.9414031
## 0.9405025
## 0.9380734
## 0.9456856
## 0.9438986
## 0.9419994
## 0.9438642
## 0.9426000
## 0.9439780
## 0.9007223
## 0.8964381
## 0.8897615
## 0.9027951
## 0.8931520
## 0.8886910
## 0.9030461
## 0.9014362
## 0.8982364
## 0.9363059
## 0.9334254
## 0.9311383
## 0.9361883
## 0.9357131
## 0.9320657
## 0.9353688
## 0.9333607
## 0.9334467
## 0.8999756
## 0.8997888
## 0.8983861
## 0.8991356
## 0.8998960
## 0.9013529
## 0.8990428
## 0.9023340
## 0.9004889
## 0.9387165
## 0.9332663
## 0.9345567
## 0.9393855
## 0.9389455
## 0.9380863
## 0.9401366
## 0.9361847
## 0.9361724
## 0.9021263
## 0.9017938
## 0.9010613
## 0.9025263
## 0.9043436
## 0.9024744
## 0.9069828
## 0.9059579
## 0.9031829
## 0.9424523
## 0.9442537
## 0.9410193
## 0.9447486
## 0.9397683
## 0.9388701
## 0.9449064
## 0.9454375
## 0.9422358
##
## Tuning parameter 'gamma' was held constant at a value of 0
##
## Tuning parameter 'min_child_weight' was held constant at a value of 1
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were nrounds = 50, max_depth = 3,
## eta = 0.3, gamma = 0, colsample_bytree = 0.8, min_child_weight = 1
## and subsample = 0.75.- Feature Importance
importance <- varImp(model_xgb, scale = TRUE)
plot(importance)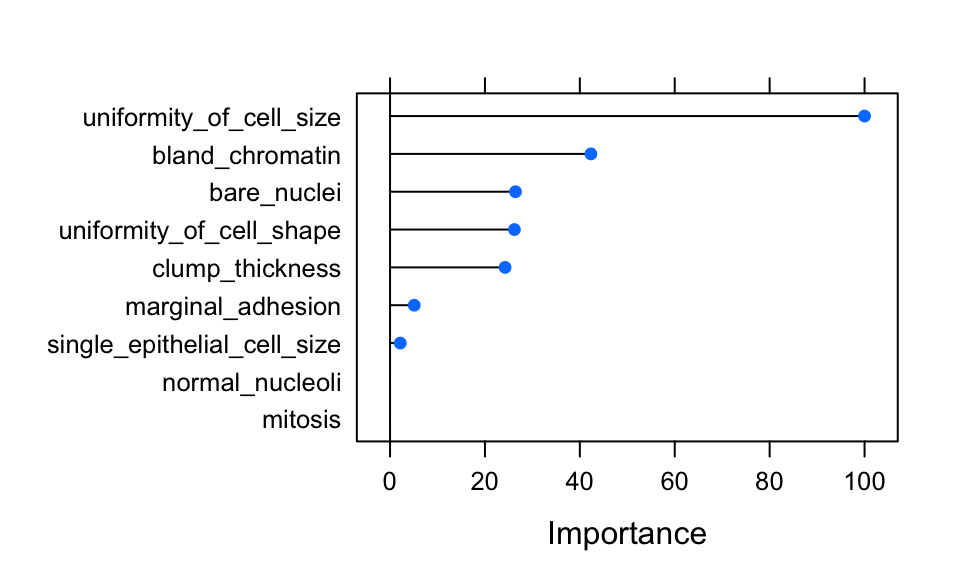
- predicting test data
confusionMatrix(predict(model_xgb, test_data), as.factor(test_data$classes))## Confusion Matrix and Statistics
##
## Reference
## Prediction benign malignant
## benign 128 3
## malignant 5 68
##
## Accuracy : 0.9608
## 95% CI : (0.9242, 0.9829)
## No Information Rate : 0.652
## P-Value [Acc > NIR] : <2e-16
##
## Kappa : 0.9142
## Mcnemar's Test P-Value : 0.7237
##
## Sensitivity : 0.9624
## Specificity : 0.9577
## Pos Pred Value : 0.9771
## Neg Pred Value : 0.9315
## Prevalence : 0.6520
## Detection Rate : 0.6275
## Detection Prevalence : 0.6422
## Balanced Accuracy : 0.9601
##
## 'Positive' Class : benign
## results <- data.frame(actual = test_data$classes,
predict(model_xgb, test_data, type = "prob"))
results$prediction <- ifelse(results$benign > 0.5, "benign",
ifelse(results$malignant > 0.5, "malignant", NA))
results$correct <- ifelse(results$actual == results$prediction, TRUE, FALSE)
ggplot(results, aes(x = prediction, fill = correct)) +
geom_bar(position = "dodge")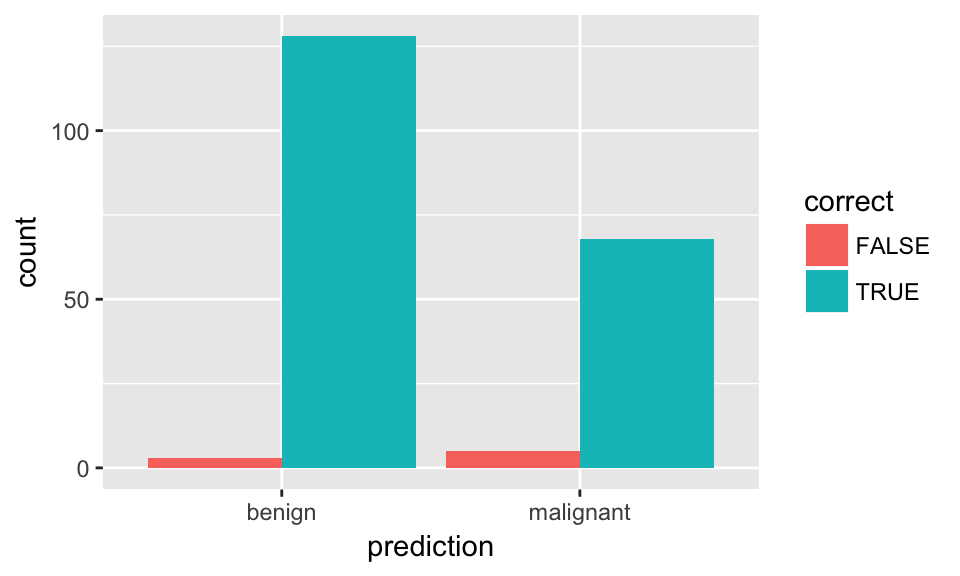
ggplot(results, aes(x = prediction, y = benign, color = correct, shape = correct)) +
geom_jitter(size = 3, alpha = 0.6)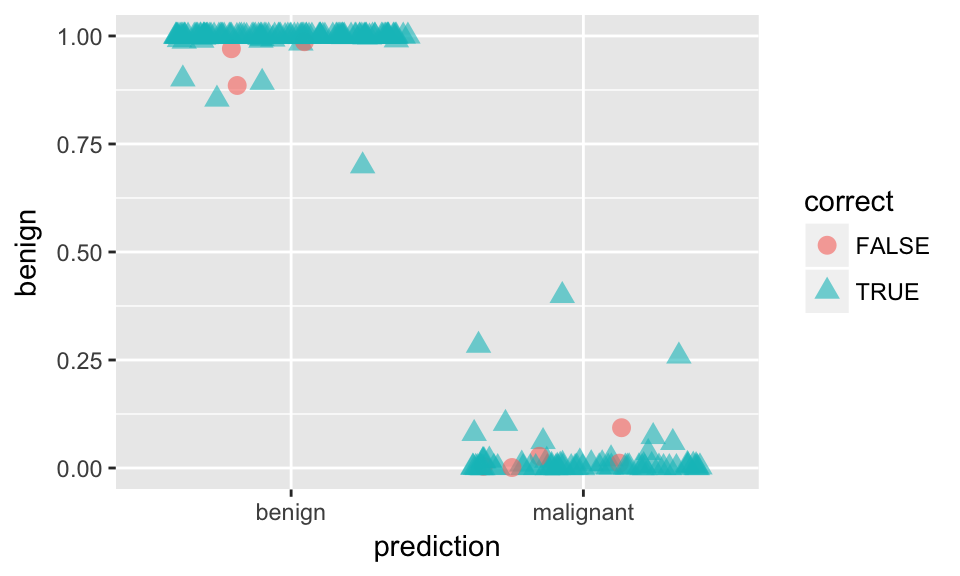
Available models in caret
https://topepo.github.io/caret/available-models.html
Feature Selection
Performing feature selection on the whole dataset would lead to prediction bias, we therefore need to run the whole modeling process on the training data alone!
- Correlation
Correlations between all features are calculated and visualised with the corrplot package. I am then removing all features with a correlation higher than 0.7, keeping the feature with the lower mean.
library(corrplot)
# calculate correlation matrix
corMatMy <- cor(train_data[, -1])
corrplot(corMatMy, order = "hclust")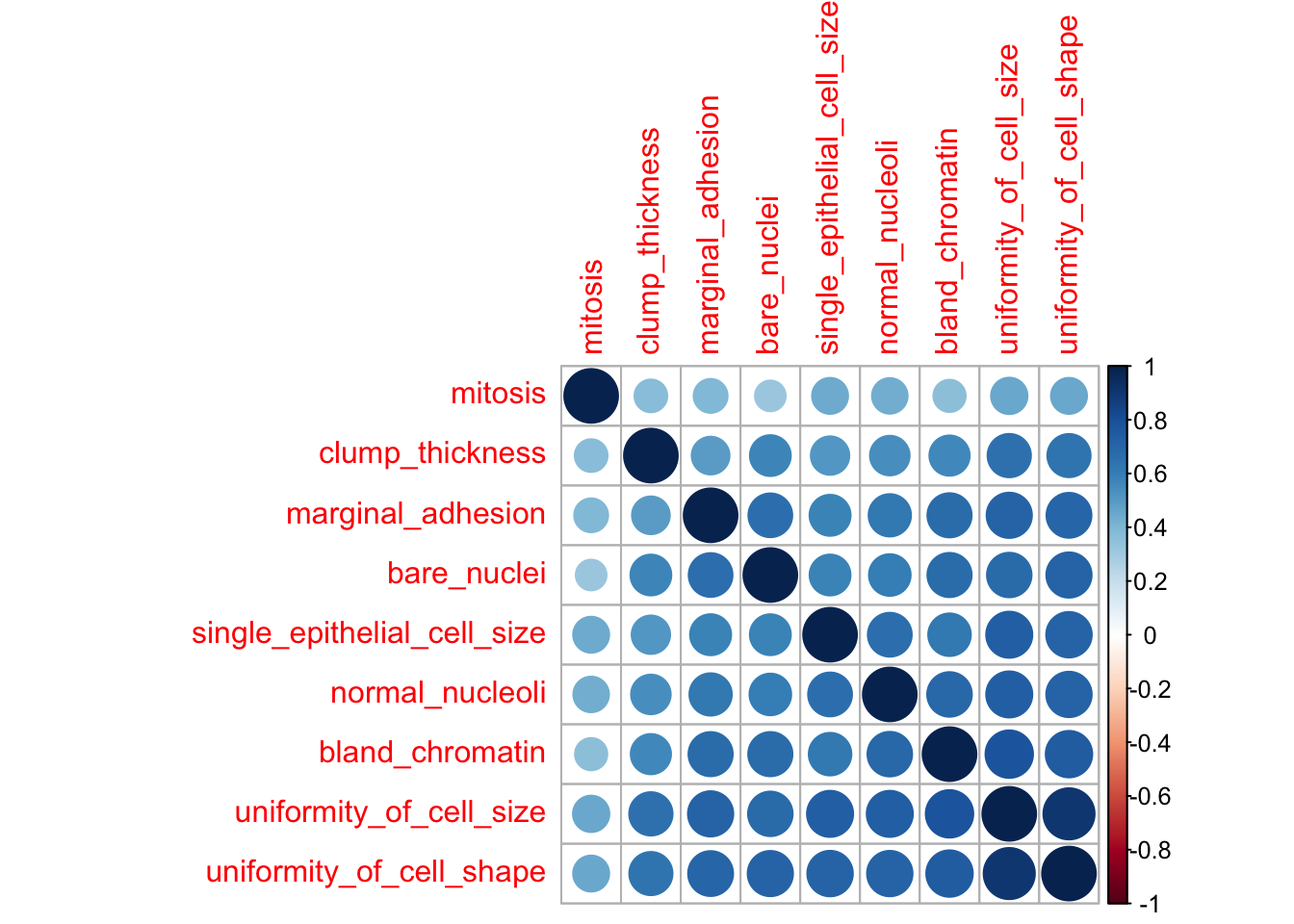
#Apply correlation filter at 0.70,
highlyCor <- colnames(train_data[, -1])[findCorrelation(corMatMy, cutoff = 0.7, verbose = TRUE)]## Compare row 2 and column 3 with corr 0.908
## Means: 0.709 vs 0.594 so flagging column 2
## Compare row 3 and column 7 with corr 0.749
## Means: 0.67 vs 0.569 so flagging column 3
## All correlations <= 0.7# which variables are flagged for removal?
highlyCor## [1] "uniformity_of_cell_size" "uniformity_of_cell_shape"#then we remove these variables
train_data_cor <- train_data[, which(!colnames(train_data) %in% highlyCor)]- Recursive Feature Elimination (RFE)
Another way to choose features is with Recursive Feature Elimination. RFE uses a Random Forest algorithm to test combinations of features and rate each with an accuracy score. The combination with the highest score is usually preferential.
set.seed(7)
results_rfe <- rfe(x = train_data[, -1],
y = as.factor(train_data$classes),
sizes = c(1:9),
rfeControl = rfeControl(functions = rfFuncs, method = "cv", number = 10))# chosen features
predictors(results_rfe)## [1] "bare_nuclei" "clump_thickness"
## [3] "uniformity_of_cell_size" "uniformity_of_cell_shape"
## [5] "bland_chromatin" "normal_nucleoli"
## [7] "marginal_adhesion" "single_epithelial_cell_size"train_data_rfe <- train_data[, c(1, which(colnames(train_data) %in% predictors(results_rfe)))]- Genetic Algorithm (GA)
The Genetic Algorithm (GA) has been developed based on evolutionary principles of natural selection: It aims to optimize a population of individuals with a given set of genotypes by modeling selection over time. In each generation (i.e. iteration), each individual’s fitness is calculated based on their genotypes. Then, the fittest individuals are chosen to produce the next generation. This subsequent generation of individuals will have genotypes resulting from (re-) combinations of the parental alleles. These new genotypes will again determine each individual’s fitness. This selection process is iterated for a specified number of generations and (ideally) leads to fixation of the fittest alleles in the gene pool.
This concept of optimization can be applied to non-evolutionary models as well, like feature selection processes in machine learning.
set.seed(27)
model_ga <- gafs(x = train_data[, -1],
y = as.factor(train_data$classes),
iters = 10, # generations of algorithm
popSize = 10, # population size for each generation
levels = c("malignant", "benign"),
gafsControl = gafsControl(functions = rfGA, # Assess fitness with RF
method = "cv", # 10 fold cross validation
genParallel = TRUE, # Use parallel programming
allowParallel = TRUE))plot(model_ga) # Plot mean fitness (AUC) by generation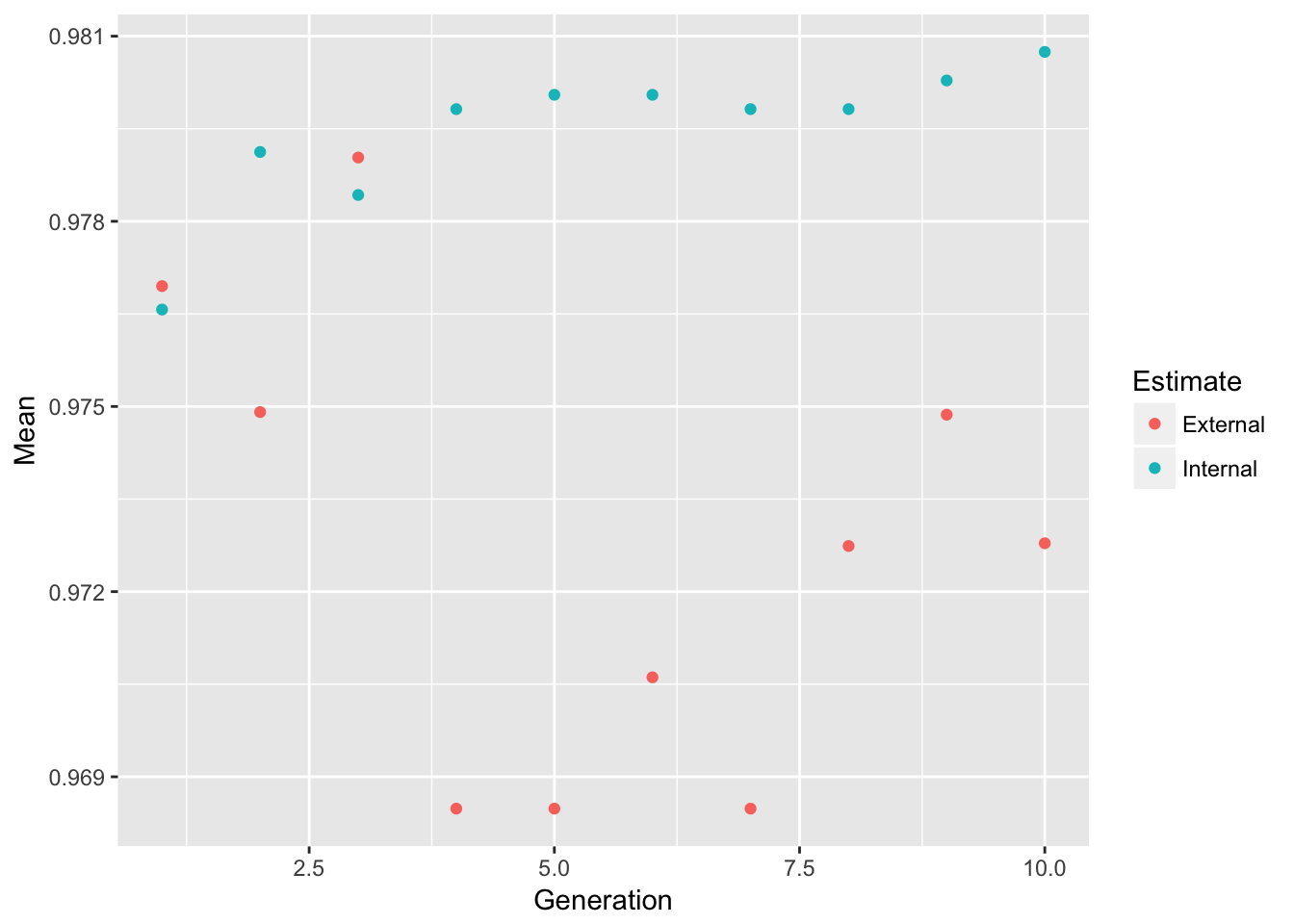
train_data_ga <- train_data[, c(1, which(colnames(train_data) %in% model_ga$ga$final))]Hyperparameter tuning with caret
Cartesian Grid
mtry: Number of variables randomly sampled as candidates at each split.
set.seed(42)
grid <- expand.grid(mtry = c(1:10))
model_rf_tune_man <- caret::train(classes ~ .,
data = train_data,
method = "rf",
preProcess = c("scale", "center"),
trControl = trainControl(method = "repeatedcv",
number = 10,
repeats = 10,
savePredictions = TRUE,
verboseIter = FALSE),
tuneGrid = grid)model_rf_tune_man## Random Forest
##
## 479 samples
## 9 predictor
## 2 classes: 'benign', 'malignant'
##
## Pre-processing: scaled (9), centered (9)
## Resampling: Cross-Validated (10 fold, repeated 10 times)
## Summary of sample sizes: 432, 431, 431, 431, 431, 431, ...
## Resampling results across tuning parameters:
##
## mtry Accuracy Kappa
## 1 0.9785044 0.9532161
## 2 0.9772586 0.9504377
## 3 0.9774625 0.9508246
## 4 0.9766333 0.9488778
## 5 0.9753789 0.9460274
## 6 0.9737078 0.9422613
## 7 0.9730957 0.9408547
## 8 0.9714155 0.9371611
## 9 0.9718280 0.9380578
## 10 0.9718280 0.9380135
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 1.plot(model_rf_tune_man)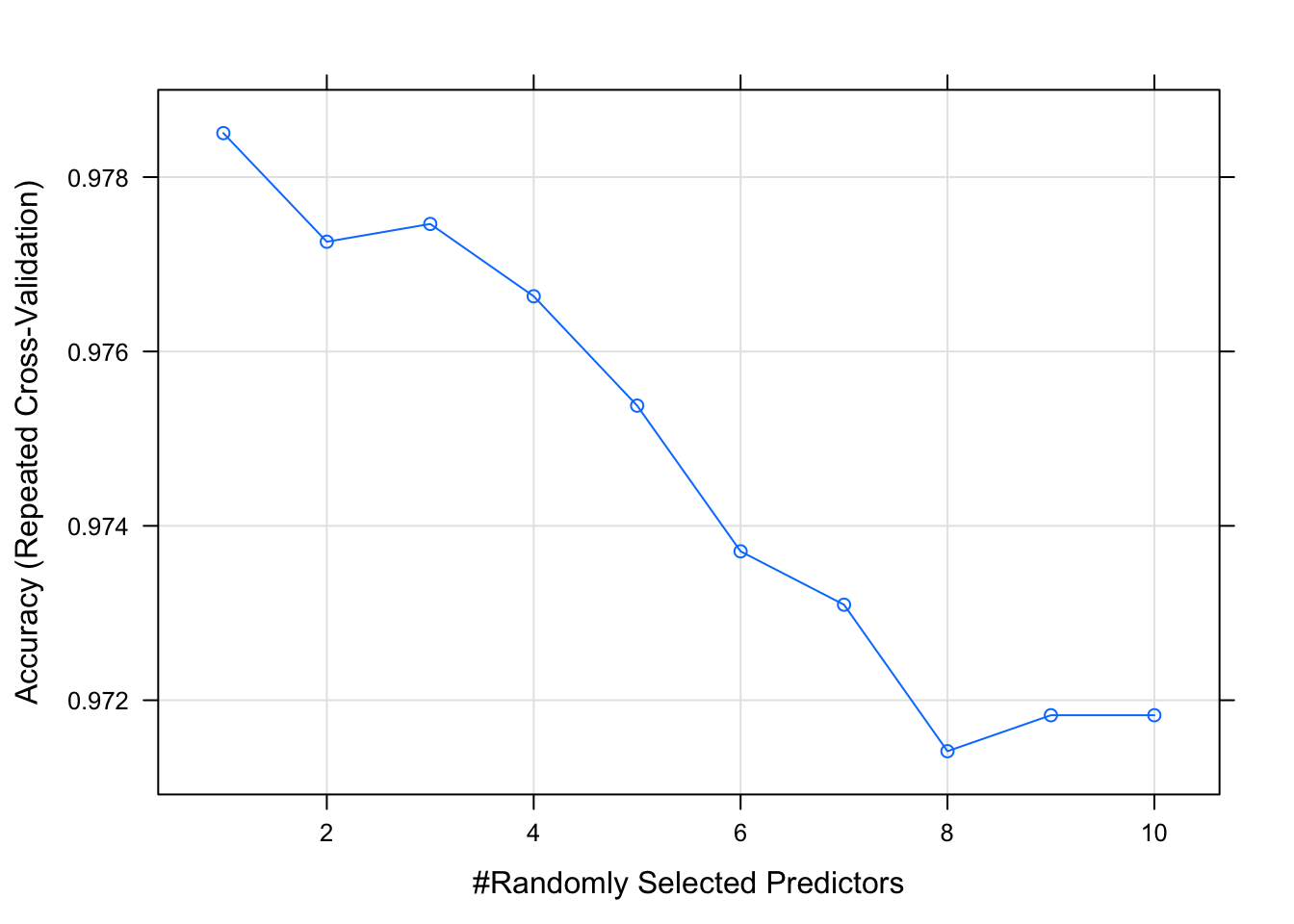
- Random Search
set.seed(42)
model_rf_tune_auto <- caret::train(classes ~ .,
data = train_data,
method = "rf",
preProcess = c("scale", "center"),
trControl = trainControl(method = "repeatedcv",
number = 10,
repeats = 10,
savePredictions = TRUE,
verboseIter = FALSE,
search = "random"),
tuneGrid = grid,
tuneLength = 15)model_rf_tune_auto## Random Forest
##
## 479 samples
## 9 predictor
## 2 classes: 'benign', 'malignant'
##
## Pre-processing: scaled (9), centered (9)
## Resampling: Cross-Validated (10 fold, repeated 10 times)
## Summary of sample sizes: 432, 431, 431, 431, 431, 431, ...
## Resampling results across tuning parameters:
##
## mtry Accuracy Kappa
## 1 0.9785044 0.9532161
## 2 0.9772586 0.9504377
## 3 0.9774625 0.9508246
## 4 0.9766333 0.9488778
## 5 0.9753789 0.9460274
## 6 0.9737078 0.9422613
## 7 0.9730957 0.9408547
## 8 0.9714155 0.9371611
## 9 0.9718280 0.9380578
## 10 0.9718280 0.9380135
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 1.plot(model_rf_tune_auto)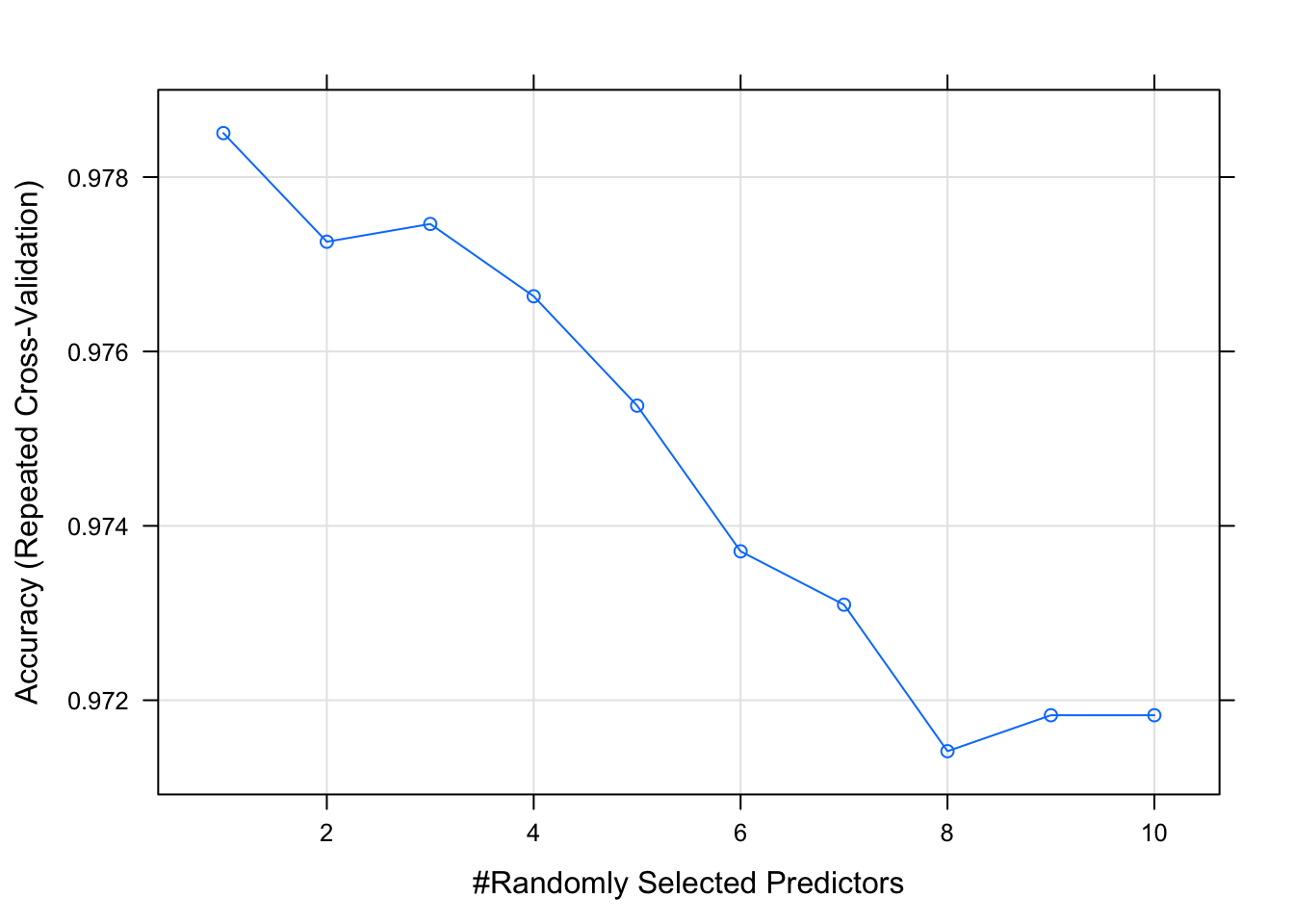
Grid search with h2o
The R package h2o provides a convenient interface to H2O, which is an open-source machine learning and deep learning platform. H2O distributes a wide range of common machine learning algorithms for classification, regression and deep learning.
library(h2o)
h2o.init(nthreads = -1)## Connection successful!
##
## R is connected to the H2O cluster:
## H2O cluster uptime: 3 days 4 minutes
## H2O cluster timezone: Europe/Berlin
## H2O data parsing timezone: UTC
## H2O cluster version: 3.20.0.2
## H2O cluster version age: 16 days
## H2O cluster name: H2O_started_from_R_shiringlander_jrj894
## H2O cluster total nodes: 1
## H2O cluster total memory: 3.27 GB
## H2O cluster total cores: 8
## H2O cluster allowed cores: 8
## H2O cluster healthy: TRUE
## H2O Connection ip: localhost
## H2O Connection port: 54321
## H2O Connection proxy: NA
## H2O Internal Security: FALSE
## H2O API Extensions: XGBoost, Algos, AutoML, Core V3, Core V4
## R Version: R version 3.5.0 (2018-04-23)h2o.no_progress()
bc_data_hf <- as.h2o(bc_data)h2o.describe(bc_data_hf) %>%
gather(x, y, Zeros:Sigma) %>%
mutate(group = ifelse(x %in% c("Min", "Max", "Mean"), "min, mean, max",
ifelse(x %in% c("NegInf", "PosInf"), "Inf", "sigma, zeros"))) %>%
ggplot(aes(x = Label, y = as.numeric(y), color = x)) +
geom_point(size = 4, alpha = 0.6) +
scale_color_brewer(palette = "Set1") +
theme(axis.text.x = element_text(angle = 45, vjust = 1, hjust = 1)) +
facet_grid(group ~ ., scales = "free") +
labs(x = "Feature",
y = "Value",
color = "")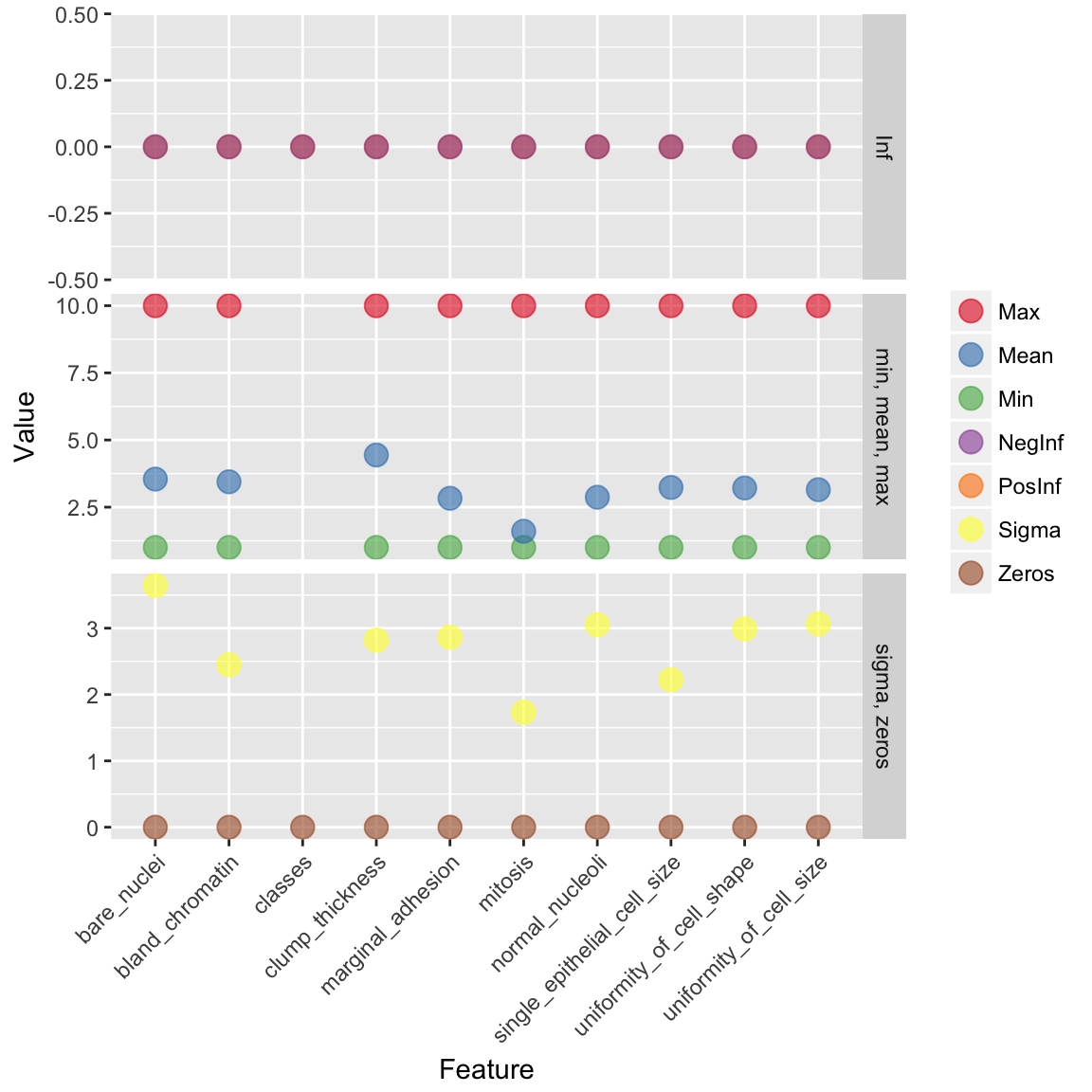
library(reshape2) # for melting
bc_data_hf[, 1] <- h2o.asfactor(bc_data_hf[, 1])
cor <- h2o.cor(bc_data_hf)
rownames(cor) <- colnames(cor)
melt(cor) %>%
mutate(Var2 = rep(rownames(cor), nrow(cor))) %>%
mutate(Var2 = factor(Var2, levels = colnames(cor))) %>%
mutate(variable = factor(variable, levels = colnames(cor))) %>%
ggplot(aes(x = variable, y = Var2, fill = value)) +
geom_tile(width = 0.9, height = 0.9) +
scale_fill_gradient2(low = "white", high = "red", name = "Cor.") +
theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust = 1)) +
labs(x = "",
y = "")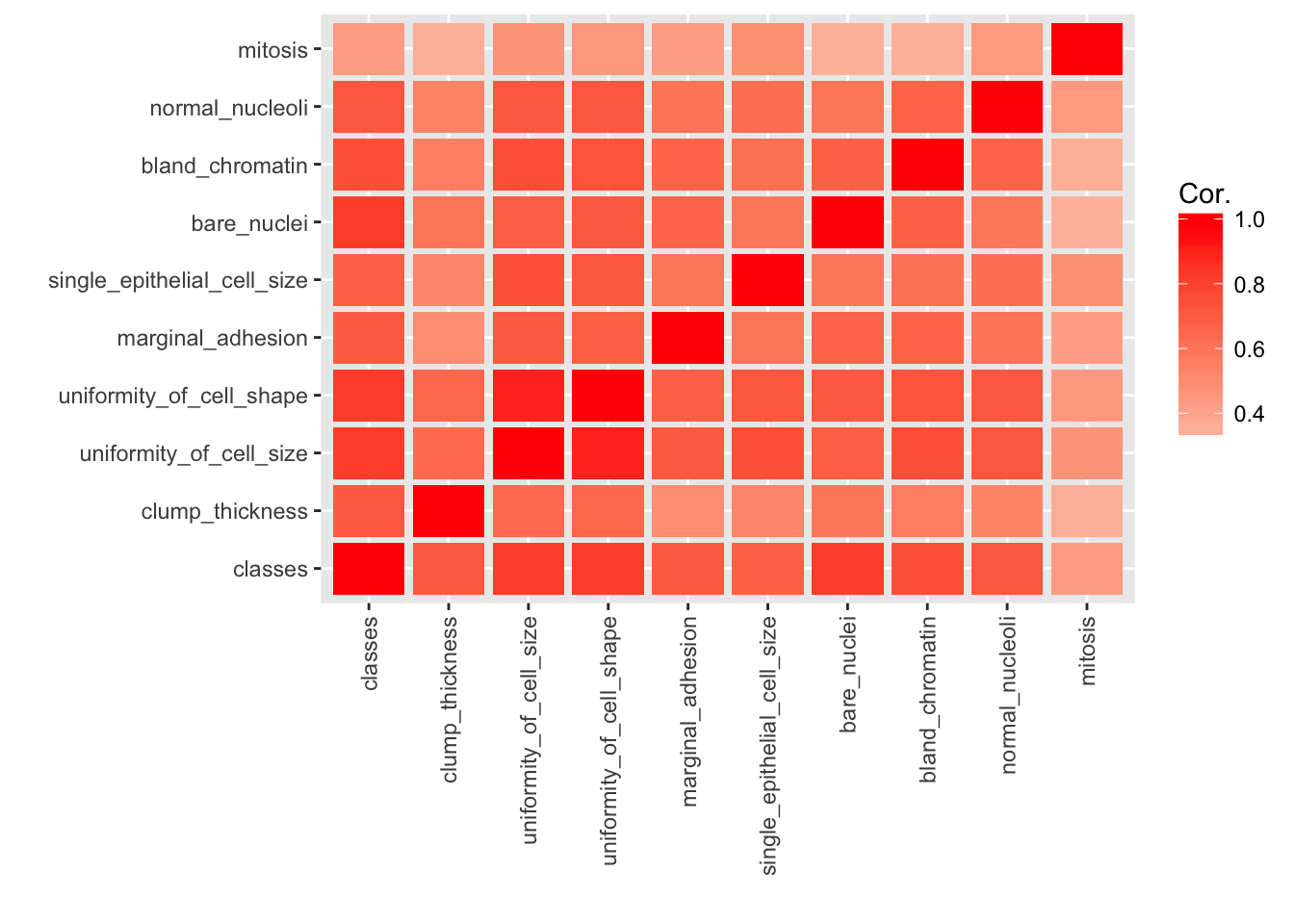
Training, validation and test data
splits <- h2o.splitFrame(bc_data_hf,
ratios = c(0.7, 0.15),
seed = 1)
train <- splits[[1]]
valid <- splits[[2]]
test <- splits[[3]]
response <- "classes"
features <- setdiff(colnames(train), response)summary(as.factor(train$classes), exact_quantiles = TRUE)## classes
## benign :313
## malignant:167summary(as.factor(valid$classes), exact_quantiles = TRUE)## classes
## benign :64
## malignant:38summary(as.factor(test$classes), exact_quantiles = TRUE)## classes
## benign :67
## malignant:34pca <- h2o.prcomp(training_frame = train,
x = features,
validation_frame = valid,
transform = "NORMALIZE",
impute_missing = TRUE,
k = 3,
seed = 42)
eigenvec <- as.data.frame(pca@model$eigenvectors)
eigenvec$label <- features
library(ggrepel)
ggplot(eigenvec, aes(x = pc1, y = pc2, label = label)) +
geom_point(color = "navy", alpha = 0.7) +
geom_text_repel()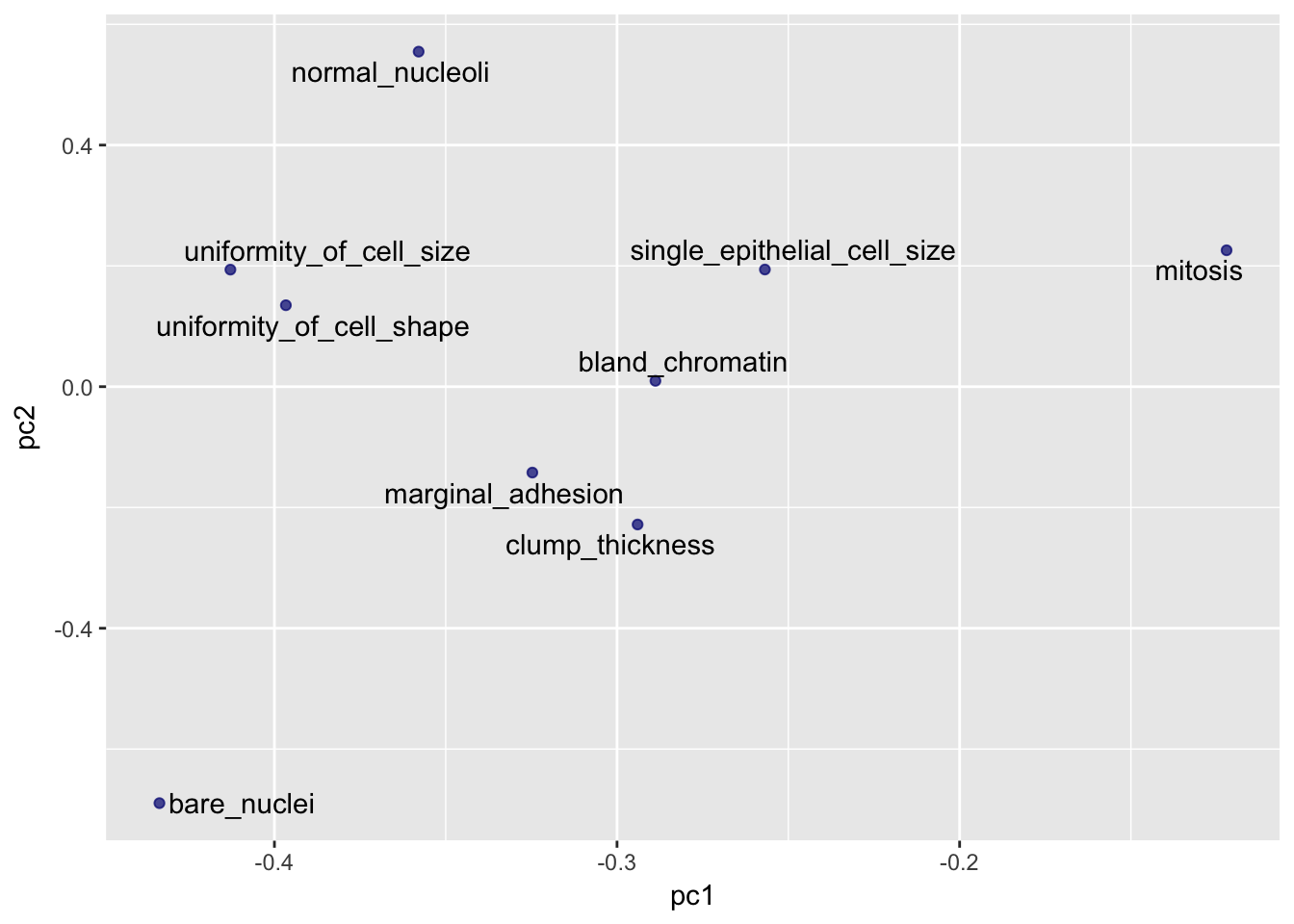
Classification
Random Forest
hyper_params <- list(
ntrees = c(25, 50, 75, 100),
max_depth = c(10, 20, 30),
min_rows = c(1, 3, 5)
)
search_criteria <- list(
strategy = "RandomDiscrete",
max_models = 50,
max_runtime_secs = 360,
stopping_rounds = 5,
stopping_metric = "AUC",
stopping_tolerance = 0.0005,
seed = 42
)rf_grid <- h2o.grid(algorithm = "randomForest", # h2o.randomForest,
# alternatively h2o.gbm
# for Gradient boosting trees
x = features,
y = response,
grid_id = "rf_grid",
training_frame = train,
validation_frame = valid,
nfolds = 25,
fold_assignment = "Stratified",
hyper_params = hyper_params,
search_criteria = search_criteria,
seed = 42
)# performance metrics where smaller is better -> order with decreasing = FALSE
sort_options_1 <- c("mean_per_class_error", "mse", "err", "logloss")
for (sort_by_1 in sort_options_1) {
grid <- h2o.getGrid("rf_grid", sort_by = sort_by_1, decreasing = FALSE)
model_ids <- grid@model_ids
best_model <- h2o.getModel(model_ids[[1]])
h2o.saveModel(best_model, path="models", force = TRUE)
}
# performance metrics where bigger is better -> order with decreasing = TRUE
sort_options_2 <- c("auc", "precision", "accuracy", "recall", "specificity")
for (sort_by_2 in sort_options_2) {
grid <- h2o.getGrid("rf_grid", sort_by = sort_by_2, decreasing = TRUE)
model_ids <- grid@model_ids
best_model <- h2o.getModel(model_ids[[1]])
h2o.saveModel(best_model, path = "models", force = TRUE)
}files <- list.files(path = "models")rf_models <- files[grep("rf_grid_model", files)]
for (model_id in rf_models) {
path <- paste0(getwd(), "/models/", model_id)
best_model <- h2o.loadModel(path)
mse_auc_test <- data.frame(model_id = model_id,
mse = h2o.mse(h2o.performance(best_model, test)),
auc = h2o.auc(h2o.performance(best_model, test)))
if (model_id == rf_models[[1]]) {
mse_auc_test_comb <- mse_auc_test
} else {
mse_auc_test_comb <- rbind(mse_auc_test_comb, mse_auc_test)
}
}mse_auc_test_comb %>%
gather(x, y, mse:auc) %>%
ggplot(aes(x = model_id, y = y, fill = model_id)) +
facet_grid(x ~ ., scales = "free") +
geom_bar(stat = "identity", alpha = 0.8, position = "dodge") +
scale_fill_brewer(palette = "Set1") +
theme(axis.text.x = element_text(angle = 45, vjust = 1, hjust = 1),
plot.margin = unit(c(0.5, 0, 0, 1.5), "cm")) +
labs(x = "", y = "value", fill = "")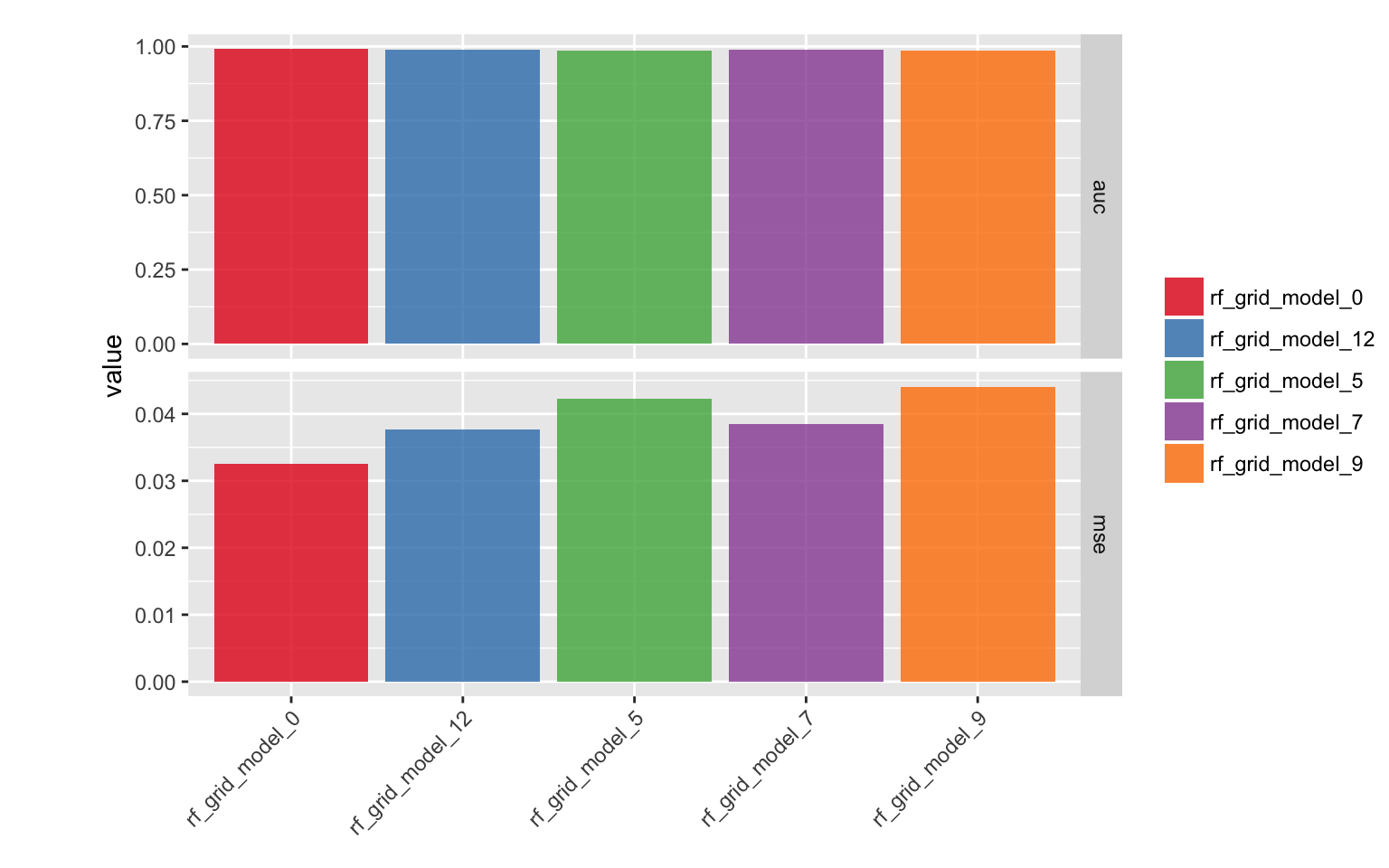
for (model_id in rf_models) {
best_model <- h2o.getModel(model_id)
finalRf_predictions <- data.frame(model_id = rep(best_model@model_id,
nrow(test)),
actual = as.vector(test$classes),
as.data.frame(h2o.predict(object = best_model,
newdata = test)))
finalRf_predictions$accurate <- ifelse(finalRf_predictions$actual ==
finalRf_predictions$predict,
"yes", "no")
finalRf_predictions$predict_stringent <- ifelse(finalRf_predictions$benign > 0.8,
"benign",
ifelse(finalRf_predictions$malignant
> 0.8, "malignant", "uncertain"))
finalRf_predictions$accurate_stringent <- ifelse(finalRf_predictions$actual ==
finalRf_predictions$predict_stringent, "yes",
ifelse(finalRf_predictions$predict_stringent ==
"uncertain", "na", "no"))
if (model_id == rf_models[[1]]) {
finalRf_predictions_comb <- finalRf_predictions
} else {
finalRf_predictions_comb <- rbind(finalRf_predictions_comb, finalRf_predictions)
}
}finalRf_predictions_comb %>%
ggplot(aes(x = actual, fill = accurate)) +
geom_bar(position = "dodge") +
scale_fill_brewer(palette = "Set1") +
facet_wrap(~ model_id, ncol = 2) +
labs(fill = "Were\npredictions\naccurate?",
title = "Default predictions")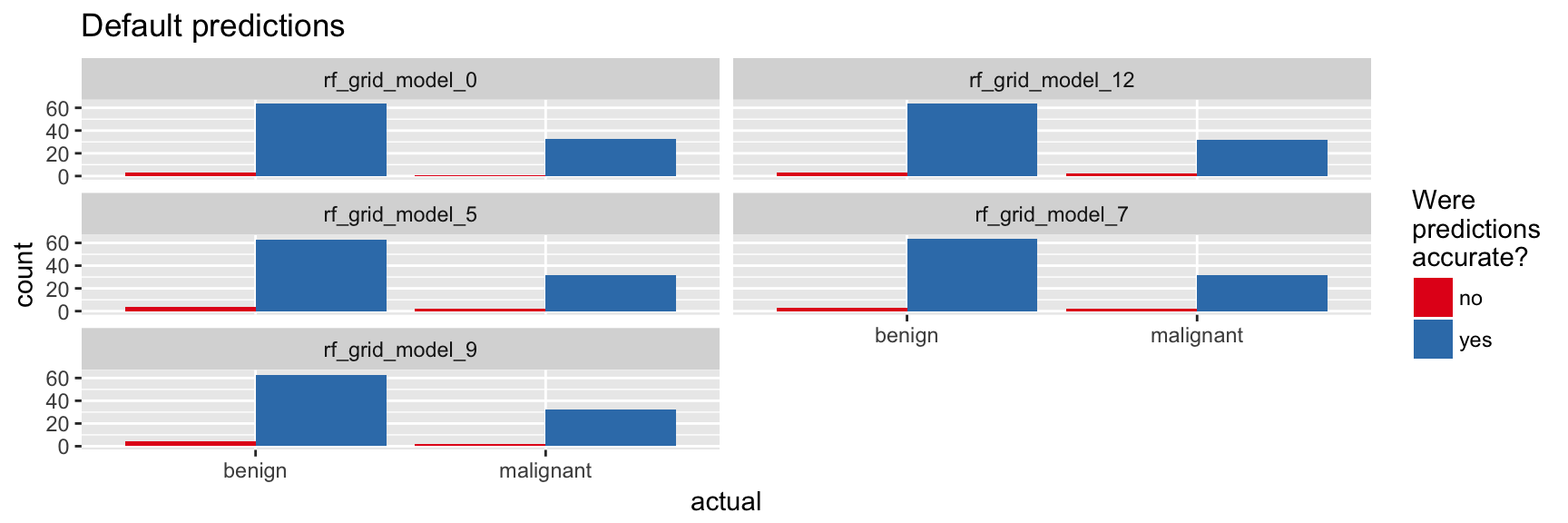
finalRf_predictions_comb %>%
subset(accurate_stringent != "na") %>%
ggplot(aes(x = actual, fill = accurate_stringent)) +
geom_bar(position = "dodge") +
scale_fill_brewer(palette = "Set1") +
facet_wrap(~ model_id, ncol = 2) +
labs(fill = "Were\npredictions\naccurate?",
title = "Stringent predictions")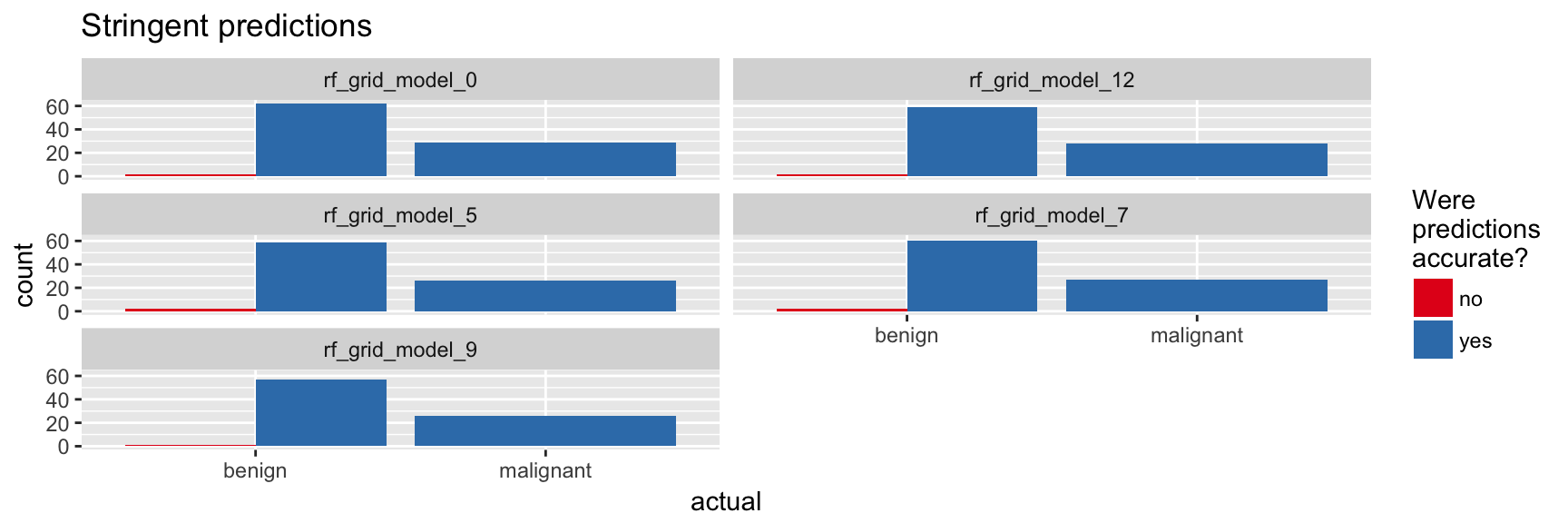
rf_model <- h2o.loadModel("models/rf_grid_model_0")h2o.varimp_plot(rf_model)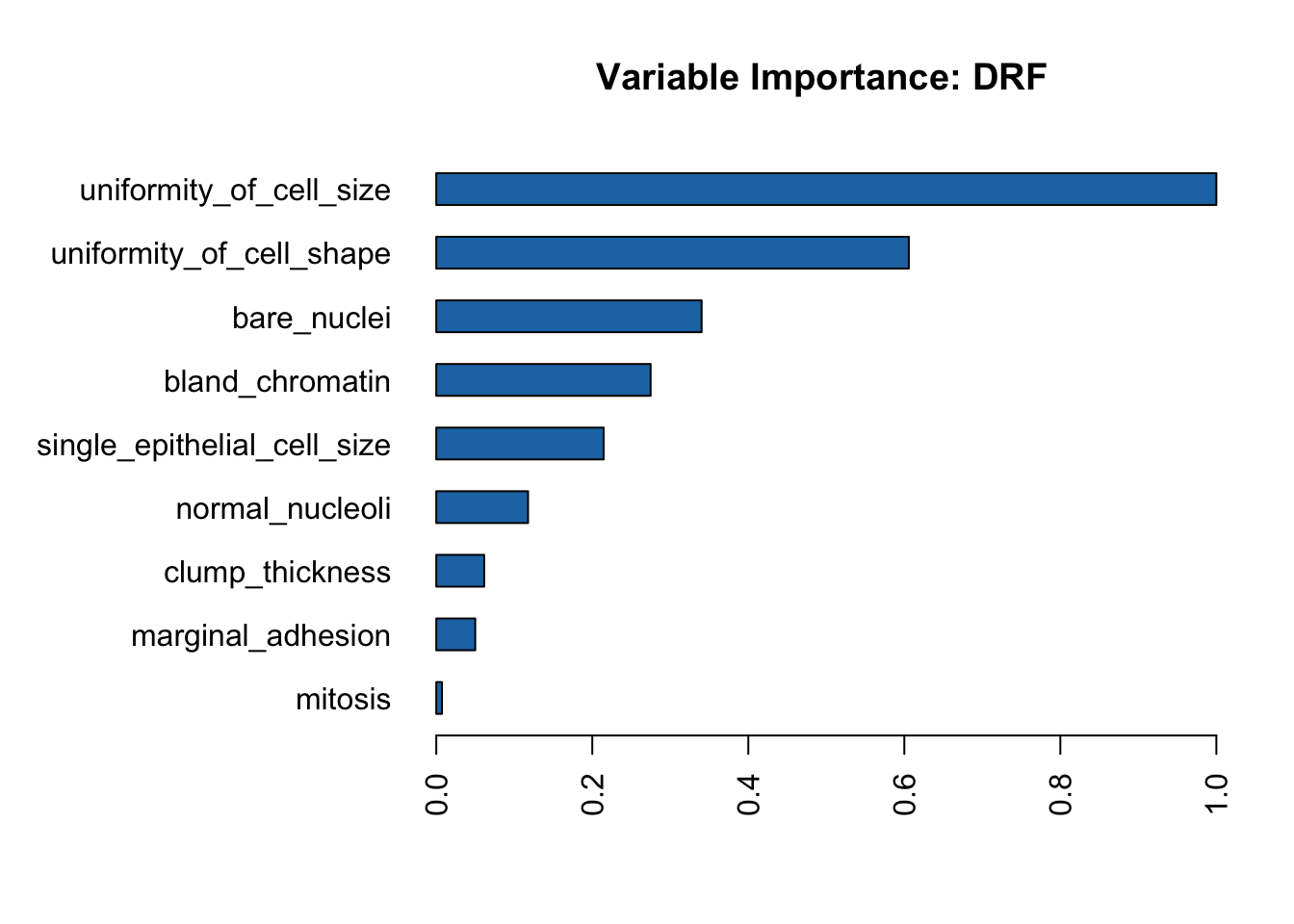
#h2o.varimp(rf_model)h2o.mean_per_class_error(rf_model, train = TRUE, valid = TRUE, xval = TRUE)## train valid xval
## 0.02196246 0.02343750 0.02515735h2o.confusionMatrix(rf_model, valid = TRUE)## Confusion Matrix (vertical: actual; across: predicted) for max f1 @ threshold = 0.533333333333333:
## benign malignant Error Rate
## benign 61 3 0.046875 =3/64
## malignant 0 38 0.000000 =0/38
## Totals 61 41 0.029412 =3/102plot(rf_model,
timestep = "number_of_trees",
metric = "classification_error")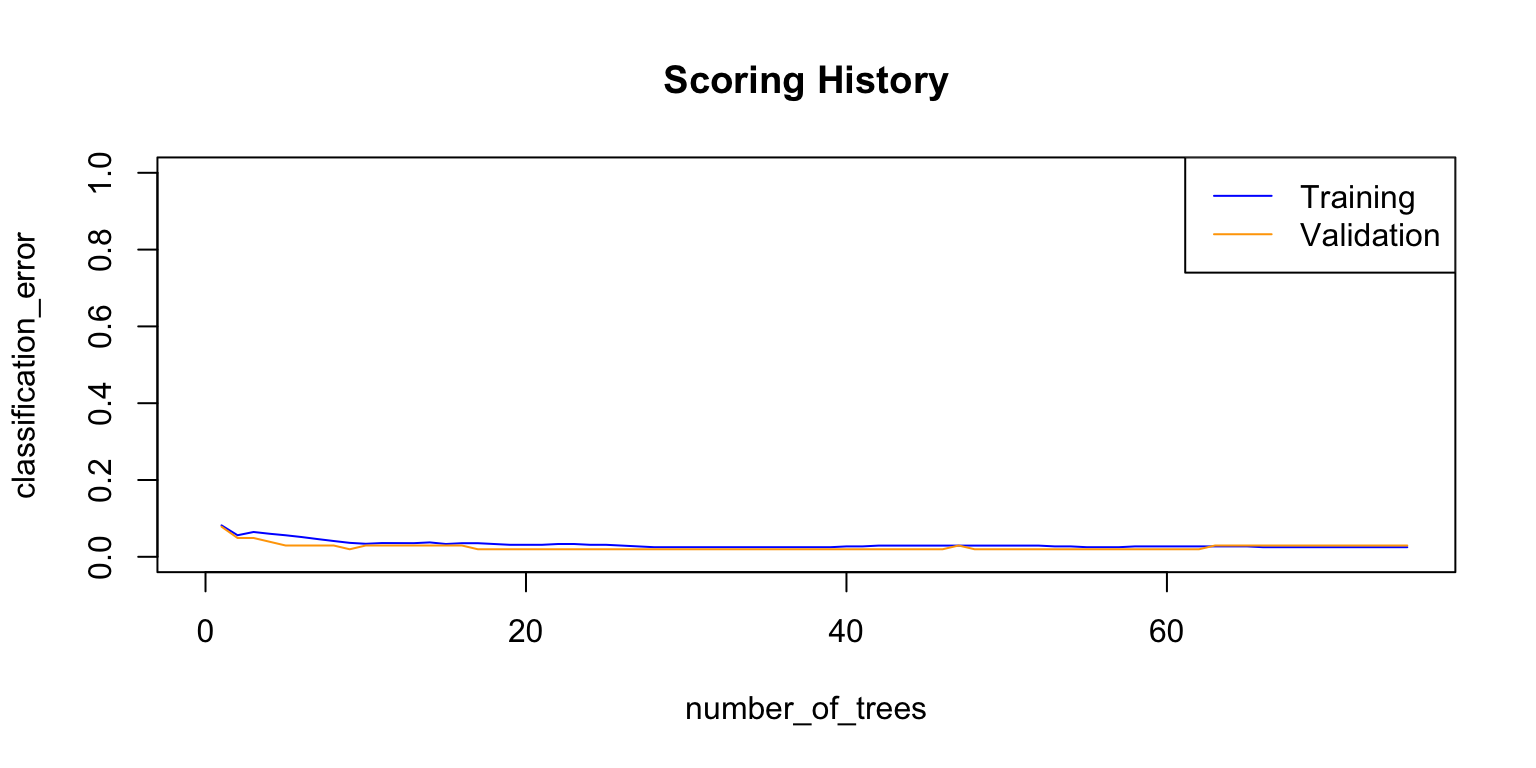
plot(rf_model,
timestep = "number_of_trees",
metric = "logloss")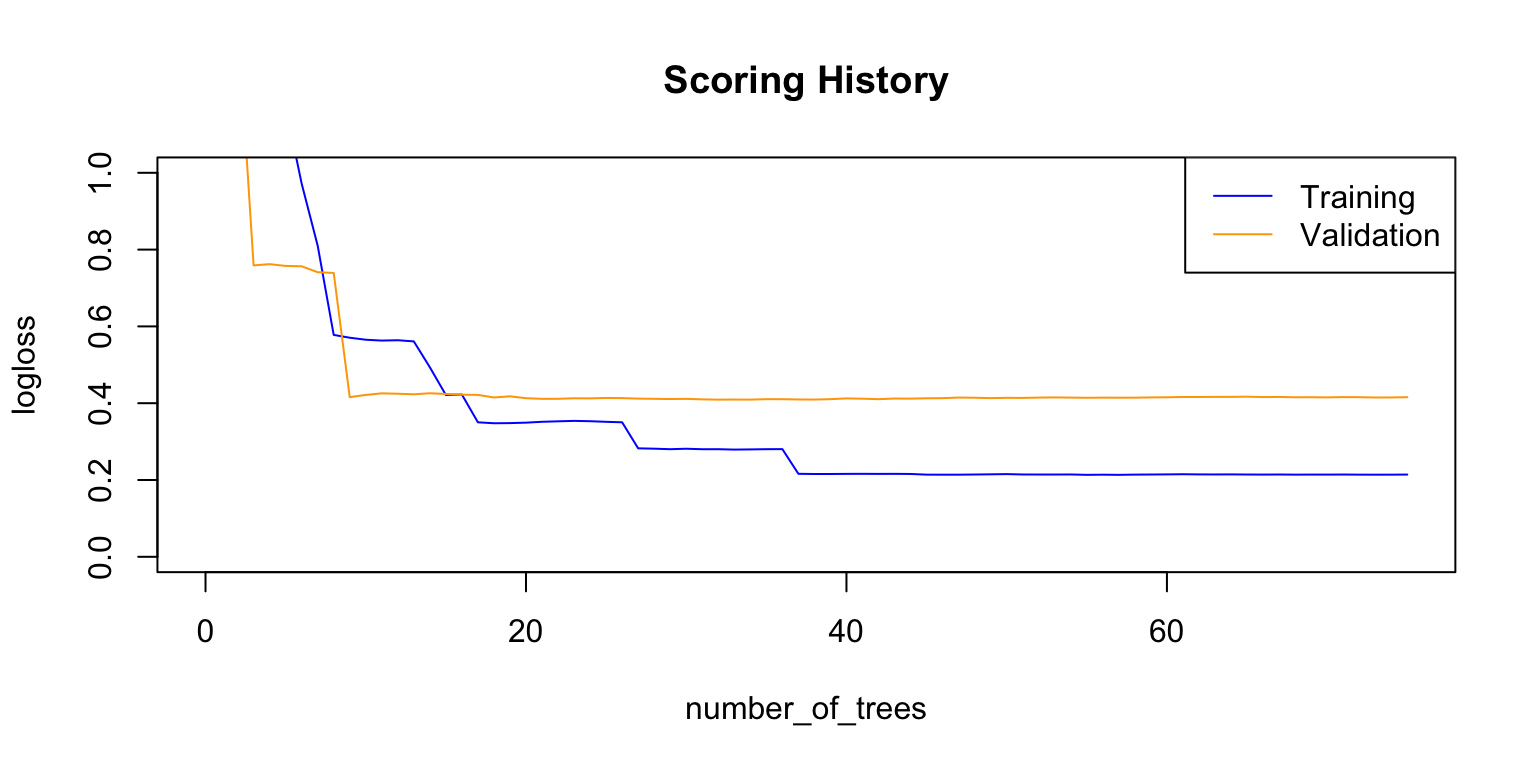
plot(rf_model,
timestep = "number_of_trees",
metric = "AUC")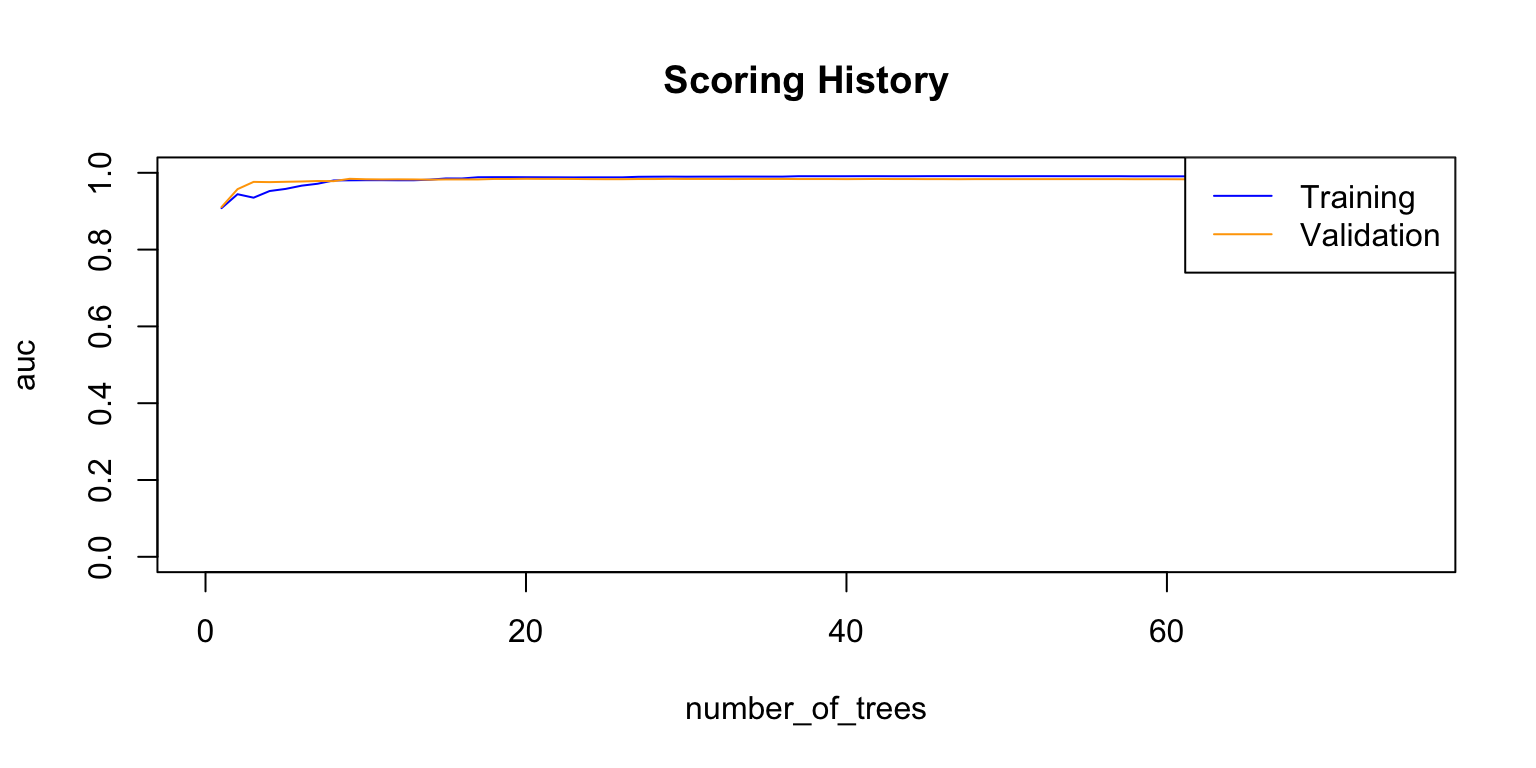
plot(rf_model,
timestep = "number_of_trees",
metric = "rmse")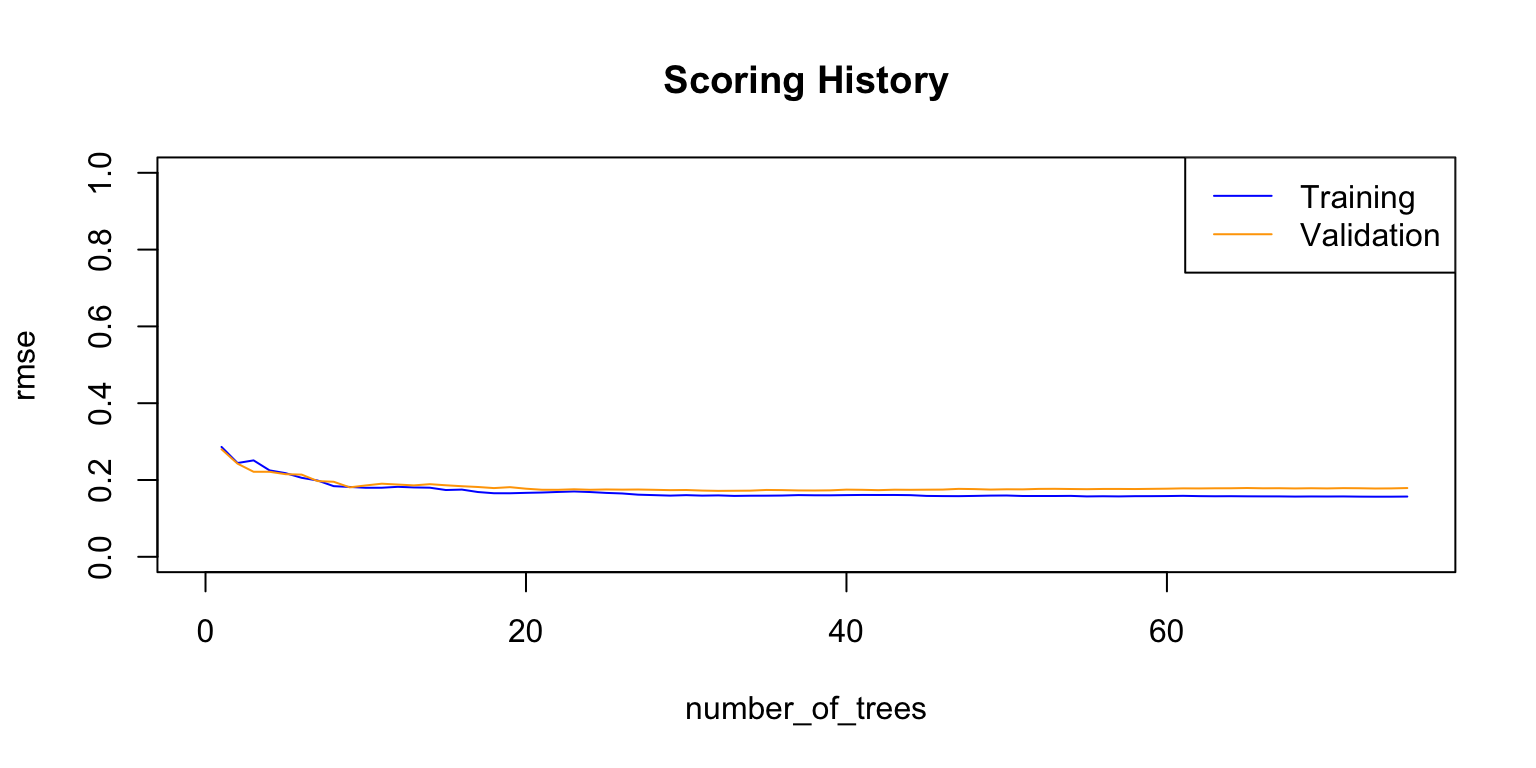
h2o.auc(rf_model, train = TRUE)## [1] 0.9907214h2o.auc(rf_model, valid = TRUE)## [1] 0.9829359h2o.auc(rf_model, xval = TRUE)## [1] 0.9903005perf <- h2o.performance(rf_model, test)
perf## H2OBinomialMetrics: drf
##
## MSE: 0.03258482
## RMSE: 0.1805127
## LogLoss: 0.1072519
## Mean Per-Class Error: 0.02985075
## AUC: 0.9916594
## Gini: 0.9833187
##
## Confusion Matrix (vertical: actual; across: predicted) for F1-optimal threshold:
## benign malignant Error Rate
## benign 63 4 0.059701 =4/67
## malignant 0 34 0.000000 =0/34
## Totals 63 38 0.039604 =4/101
##
## Maximum Metrics: Maximum metrics at their respective thresholds
## metric threshold value idx
## 1 max f1 0.306667 0.944444 18
## 2 max f2 0.306667 0.977011 18
## 3 max f0point5 0.720000 0.933735 13
## 4 max accuracy 0.533333 0.960396 16
## 5 max precision 1.000000 1.000000 0
## 6 max recall 0.306667 1.000000 18
## 7 max specificity 1.000000 1.000000 0
## 8 max absolute_mcc 0.306667 0.917235 18
## 9 max min_per_class_accuracy 0.533333 0.955224 16
## 10 max mean_per_class_accuracy 0.306667 0.970149 18
##
## Gains/Lift Table: Extract with `h2o.gainsLift(<model>, <data>)` or `h2o.gainsLift(<model>, valid=<T/F>, xval=<T/F>)`plot(perf)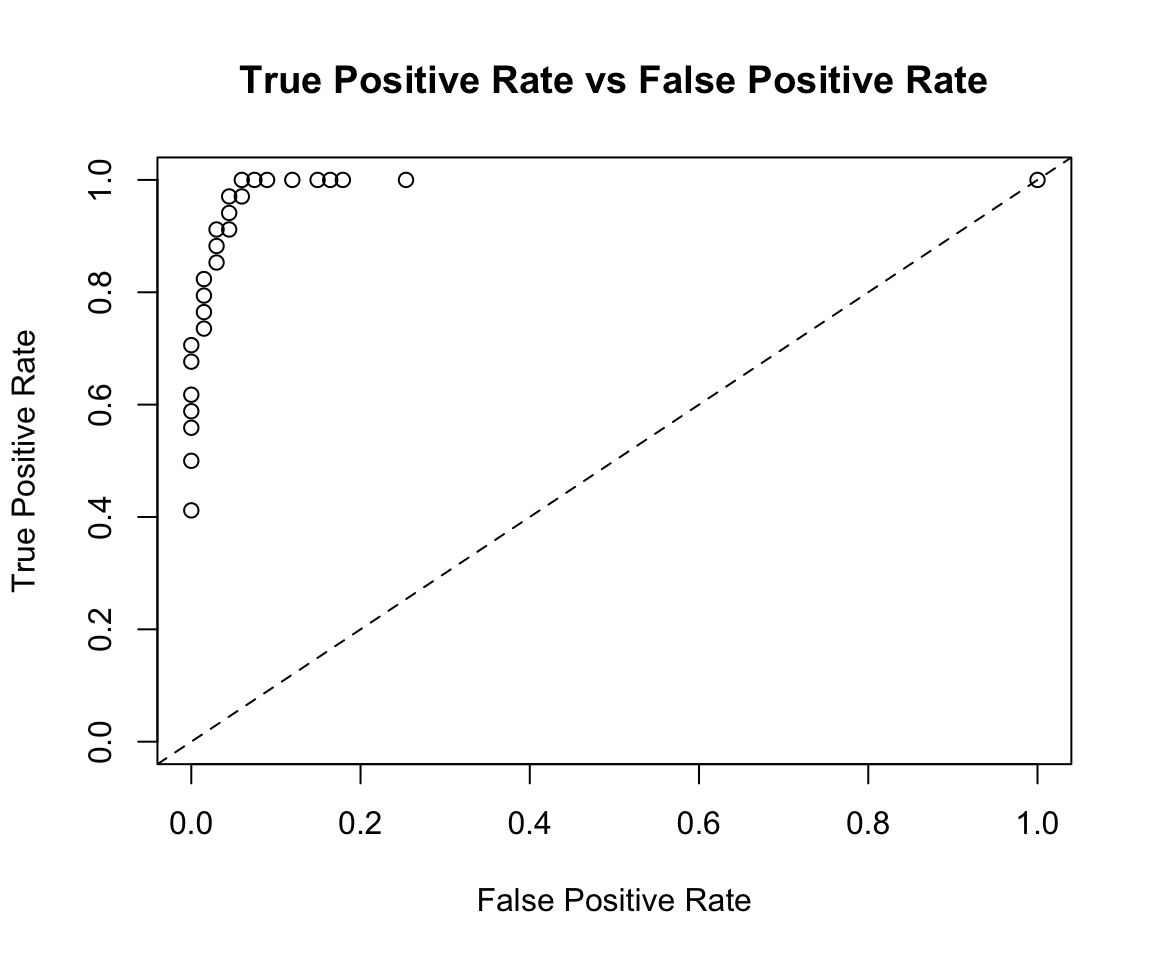
perf@metrics$thresholds_and_metric_scores %>%
ggplot(aes(x = fpr, y = tpr)) +
geom_point() +
geom_line() +
geom_abline(slope = 1, intercept = 0) +
labs(x = "False Positive Rate",
y = "True Positive Rate")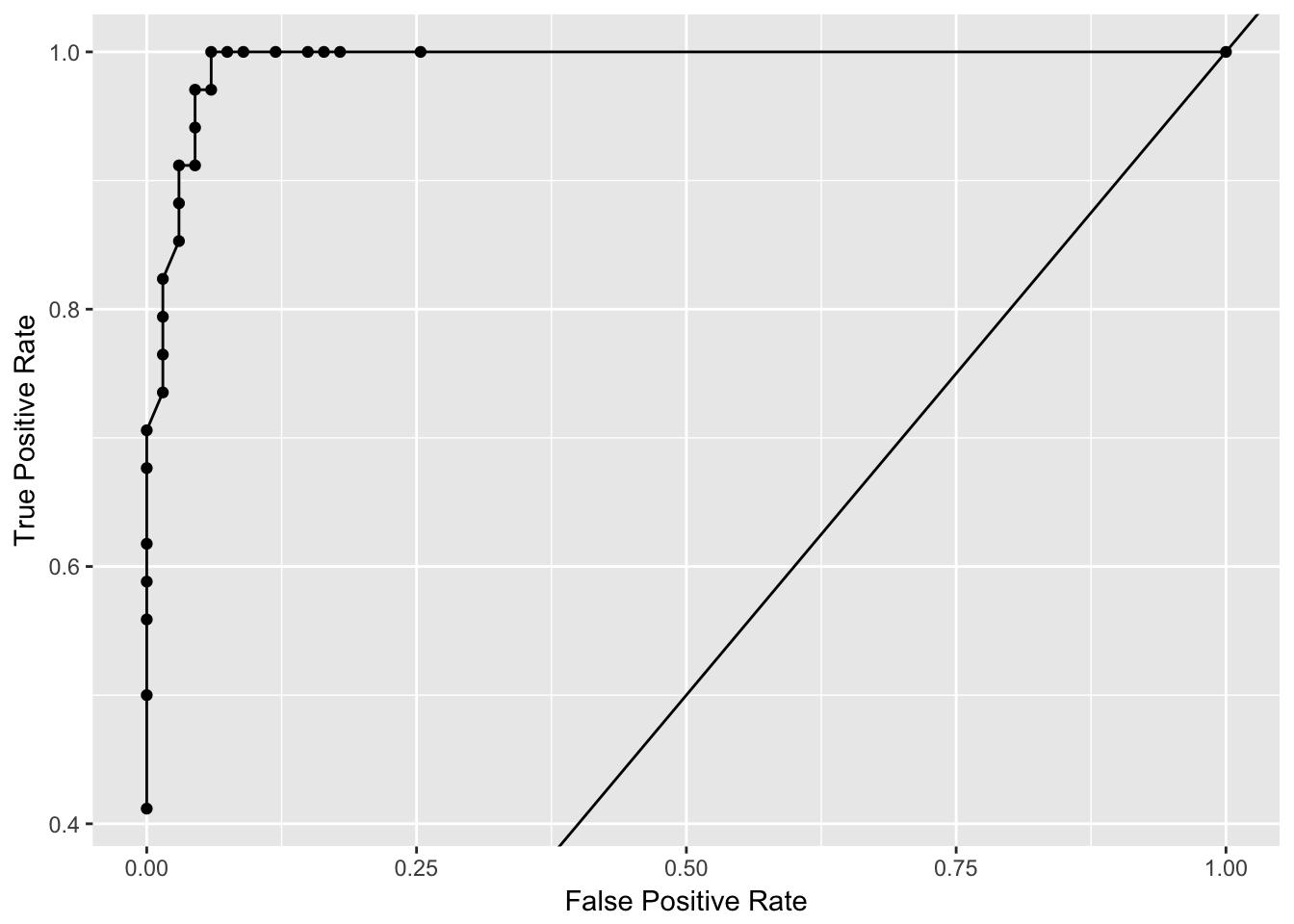
h2o.logloss(perf)## [1] 0.1072519h2o.mse(perf)## [1] 0.03258482h2o.auc(perf)## [1] 0.9916594head(h2o.metric(perf))## Metrics for Thresholds: Binomial metrics as a function of classification thresholds
## threshold f1 f2 f0point5 accuracy precision recall
## 1 1.000000 0.583333 0.466667 0.777778 0.801980 1.000000 0.411765
## 2 0.986667 0.666667 0.555556 0.833333 0.831683 1.000000 0.500000
## 3 0.973333 0.716981 0.612903 0.863636 0.851485 1.000000 0.558824
## 4 0.960000 0.740741 0.641026 0.877193 0.861386 1.000000 0.588235
## 5 0.946667 0.763636 0.668790 0.889831 0.871287 1.000000 0.617647
## 6 0.920000 0.807018 0.723270 0.912698 0.891089 1.000000 0.676471
## specificity absolute_mcc min_per_class_accuracy mean_per_class_accuracy
## 1 1.000000 0.563122 0.411765 0.705882
## 2 1.000000 0.631514 0.500000 0.750000
## 3 1.000000 0.675722 0.558824 0.779412
## 4 1.000000 0.697542 0.588235 0.794118
## 5 1.000000 0.719221 0.617647 0.808824
## 6 1.000000 0.762280 0.676471 0.838235
## tns fns fps tps tnr fnr fpr tpr idx
## 1 67 20 0 14 1.000000 0.588235 0.000000 0.411765 0
## 2 67 17 0 17 1.000000 0.500000 0.000000 0.500000 1
## 3 67 15 0 19 1.000000 0.441176 0.000000 0.558824 2
## 4 67 14 0 20 1.000000 0.411765 0.000000 0.588235 3
## 5 67 13 0 21 1.000000 0.382353 0.000000 0.617647 4
## 6 67 11 0 23 1.000000 0.323529 0.000000 0.676471 5finalRf_predictions <- data.frame(actual = as.vector(test$classes),
as.data.frame(h2o.predict(object = rf_model,
newdata = test)))
finalRf_predictions$accurate <- ifelse(finalRf_predictions$actual ==
finalRf_predictions$predict, "yes", "no")
finalRf_predictions$predict_stringent <- ifelse(finalRf_predictions$benign > 0.8, "benign",
ifelse(finalRf_predictions$malignant
> 0.8, "malignant", "uncertain"))
finalRf_predictions$accurate_stringent <- ifelse(finalRf_predictions$actual ==
finalRf_predictions$predict_stringent, "yes",
ifelse(finalRf_predictions$predict_stringent ==
"uncertain", "na", "no"))
finalRf_predictions %>%
group_by(actual, predict) %>%
dplyr::summarise(n = n())## # A tibble: 4 x 3
## # Groups: actual [?]
## actual predict n
## <fct> <fct> <int>
## 1 benign benign 64
## 2 benign malignant 3
## 3 malignant benign 1
## 4 malignant malignant 33finalRf_predictions %>%
group_by(actual, predict_stringent) %>%
dplyr::summarise(n = n())## # A tibble: 5 x 3
## # Groups: actual [?]
## actual predict_stringent n
## <fct> <chr> <int>
## 1 benign benign 62
## 2 benign malignant 2
## 3 benign uncertain 3
## 4 malignant malignant 29
## 5 malignant uncertain 5finalRf_predictions %>%
ggplot(aes(x = actual, fill = accurate)) +
geom_bar(position = "dodge") +
scale_fill_brewer(palette = "Set1") +
labs(fill = "Were\npredictions\naccurate?",
title = "Default predictions")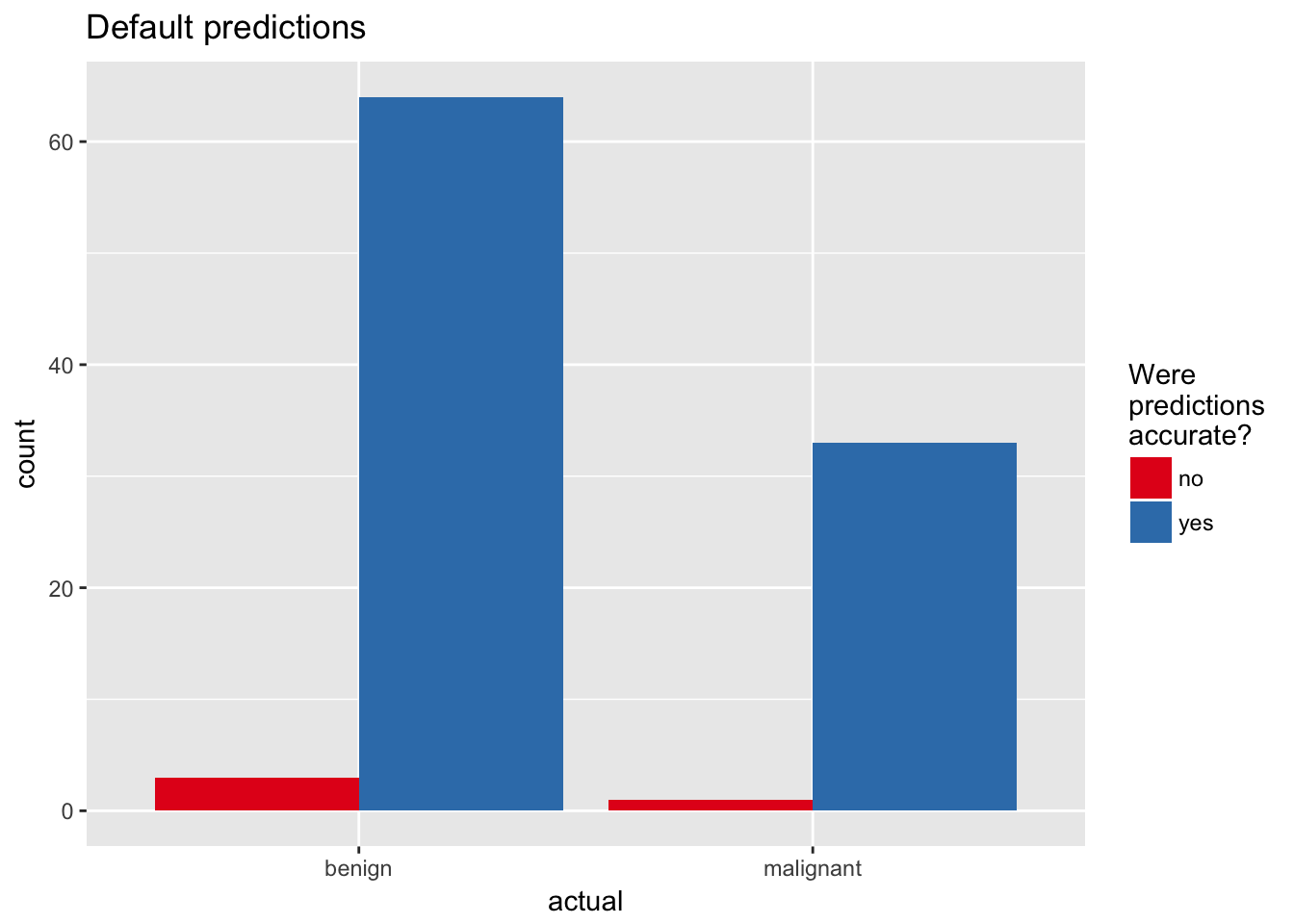
finalRf_predictions %>%
subset(accurate_stringent != "na") %>%
ggplot(aes(x = actual, fill = accurate_stringent)) +
geom_bar(position = "dodge") +
scale_fill_brewer(palette = "Set1") +
labs(fill = "Were\npredictions\naccurate?",
title = "Stringent predictions")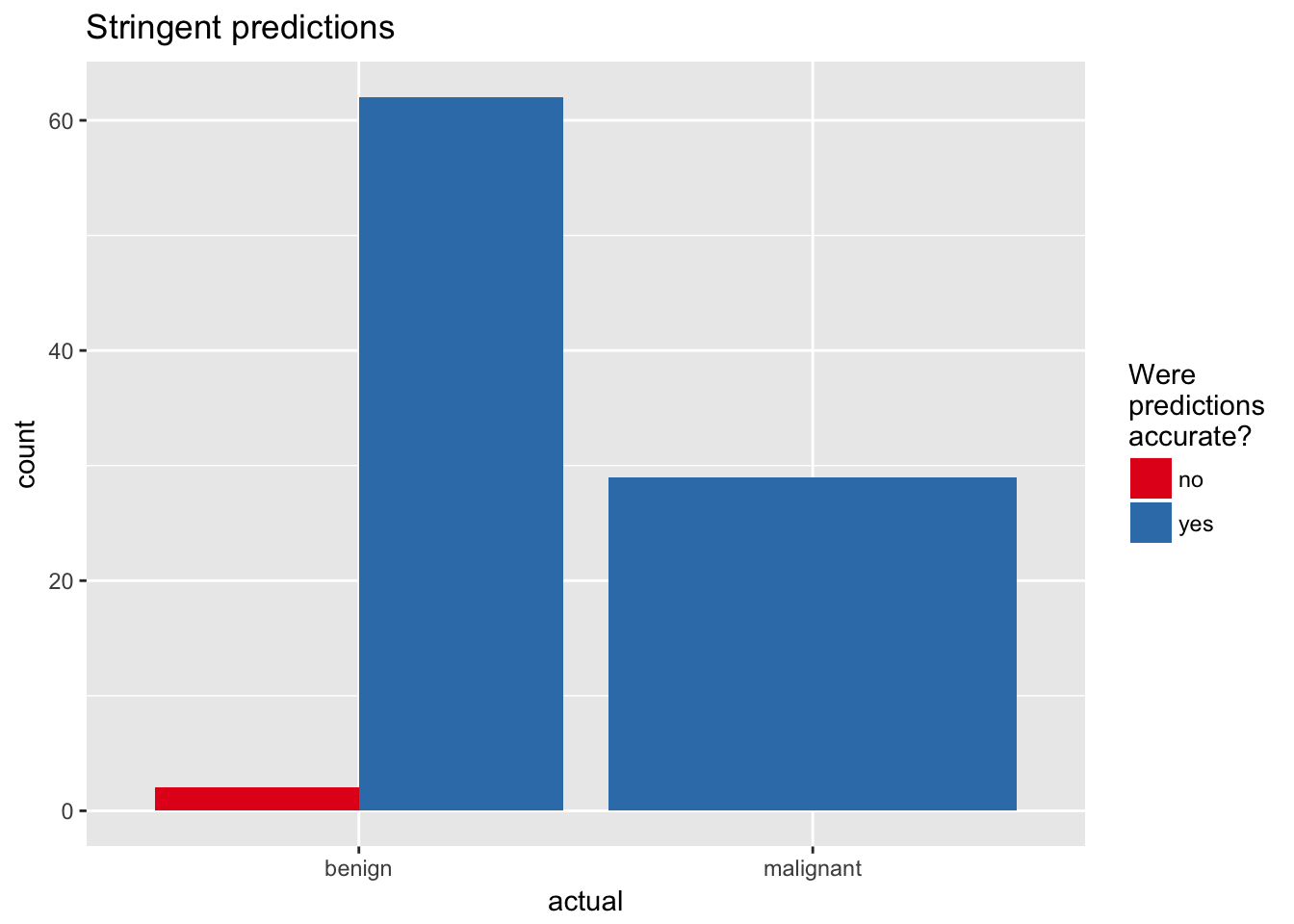
df <- finalRf_predictions[, c(1, 3, 4)]
thresholds <- seq(from = 0, to = 1, by = 0.1)
prop_table <- data.frame(threshold = thresholds, prop_true_b = NA, prop_true_m = NA)
for (threshold in thresholds) {
pred <- ifelse(df$benign > threshold, "benign", "malignant")
pred_t <- ifelse(pred == df$actual, TRUE, FALSE)
group <- data.frame(df, "pred" = pred_t) %>%
group_by(actual, pred) %>%
dplyr::summarise(n = n())
group_b <- filter(group, actual == "benign")
prop_b <- sum(filter(group_b, pred == TRUE)$n) / sum(group_b$n)
prop_table[prop_table$threshold == threshold, "prop_true_b"] <- prop_b
group_m <- filter(group, actual == "malignant")
prop_m <- sum(filter(group_m, pred == TRUE)$n) / sum(group_m$n)
prop_table[prop_table$threshold == threshold, "prop_true_m"] <- prop_m
}
prop_table %>%
gather(x, y, prop_true_b:prop_true_m) %>%
ggplot(aes(x = threshold, y = y, color = x)) +
geom_point() +
geom_line() +
scale_color_brewer(palette = "Set1") +
labs(y = "proportion of true predictions",
color = "b: benign cases\nm: malignant cases")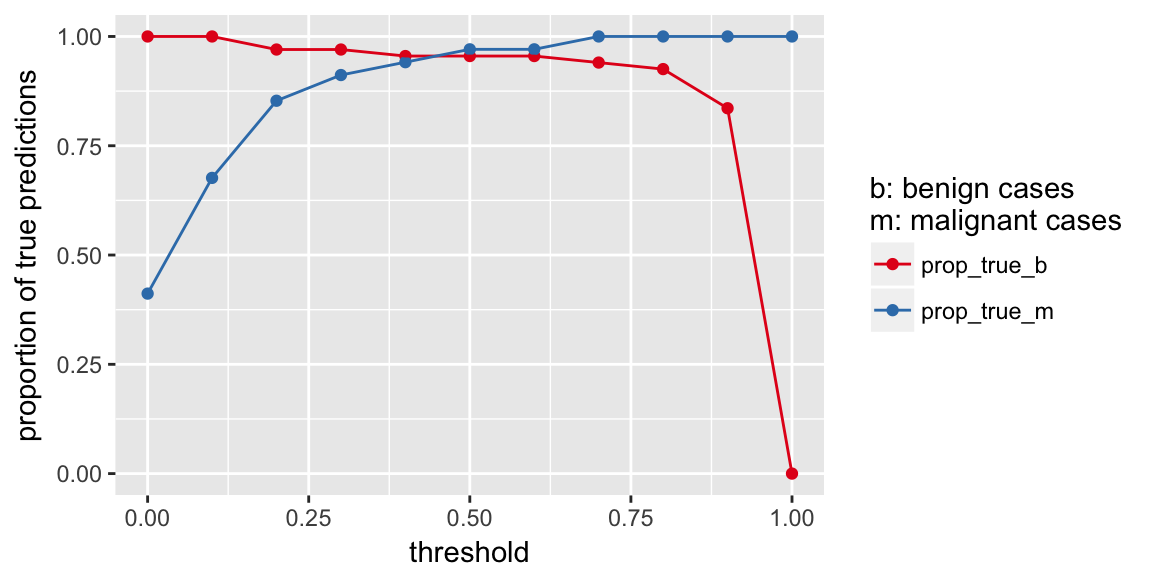
If you are interested in more machine learning posts, check out the category listing for machine_learning on my blog - https://shirinsplayground.netlify.com/categories/#posts-list-machine-learning - https://shiring.github.io/categories.html#machine_learning-ref
stopCluster(cl)
h2o.shutdown()## Are you sure you want to shutdown the H2O instance running at http://localhost:54321/ (Y/N)?sessionInfo()## R version 3.5.0 (2018-04-23)
## Platform: x86_64-apple-darwin15.6.0 (64-bit)
## Running under: macOS High Sierra 10.13.5
##
## Matrix products: default
## BLAS: /Library/Frameworks/R.framework/Versions/3.5/Resources/lib/libRblas.0.dylib
## LAPACK: /Library/Frameworks/R.framework/Versions/3.5/Resources/lib/libRlapack.dylib
##
## locale:
## [1] de_DE.UTF-8/de_DE.UTF-8/de_DE.UTF-8/C/de_DE.UTF-8/de_DE.UTF-8
##
## attached base packages:
## [1] parallel stats graphics grDevices utils datasets methods
## [8] base
##
## other attached packages:
## [1] ggrepel_0.8.0 reshape2_1.4.3 h2o_3.20.0.2
## [4] corrplot_0.84 caret_6.0-80 doParallel_1.0.11
## [7] iterators_1.0.9 foreach_1.4.4 ellipse_0.4.1
## [10] igraph_1.2.1 bindrcpp_0.2.2 mice_3.1.0
## [13] lattice_0.20-35 forcats_0.3.0 stringr_1.3.1
## [16] dplyr_0.7.5 purrr_0.2.5 readr_1.1.1
## [19] tidyr_0.8.1 tibble_1.4.2 ggplot2_2.2.1
## [22] tidyverse_1.2.1
##
## loaded via a namespace (and not attached):
## [1] minqa_1.2.4 colorspace_1.3-2 class_7.3-14
## [4] rprojroot_1.3-2 pls_2.6-0 rstudioapi_0.7
## [7] DRR_0.0.3 prodlim_2018.04.18 lubridate_1.7.4
## [10] xml2_1.2.0 codetools_0.2-15 splines_3.5.0
## [13] mnormt_1.5-5 robustbase_0.93-1 knitr_1.20
## [16] RcppRoll_0.3.0 jsonlite_1.5 nloptr_1.0.4
## [19] broom_0.4.4 ddalpha_1.3.4 kernlab_0.9-26
## [22] sfsmisc_1.1-2 compiler_3.5.0 httr_1.3.1
## [25] backports_1.1.2 assertthat_0.2.0 Matrix_1.2-14
## [28] lazyeval_0.2.1 cli_1.0.0 htmltools_0.3.6
## [31] tools_3.5.0 gtable_0.2.0 glue_1.2.0
## [34] Rcpp_0.12.17 cellranger_1.1.0 nlme_3.1-137
## [37] blogdown_0.6 psych_1.8.4 timeDate_3043.102
## [40] xfun_0.2 gower_0.1.2 lme4_1.1-17
## [43] rvest_0.3.2 pan_1.4 DEoptimR_1.0-8
## [46] MASS_7.3-50 scales_0.5.0 ipred_0.9-6
## [49] hms_0.4.2 RColorBrewer_1.1-2 yaml_2.1.19
## [52] rpart_4.1-13 stringi_1.2.3 randomForest_4.6-14
## [55] e1071_1.6-8 lava_1.6.1 geometry_0.3-6
## [58] bitops_1.0-6 rlang_0.2.1 pkgconfig_2.0.1
## [61] evaluate_0.10.1 bindr_0.1.1 recipes_0.1.3
## [64] labeling_0.3 CVST_0.2-2 tidyselect_0.2.4
## [67] plyr_1.8.4 magrittr_1.5 bookdown_0.7
## [70] R6_2.2.2 mitml_0.3-5 dimRed_0.1.0
## [73] pillar_1.2.3 haven_1.1.1 foreign_0.8-70
## [76] withr_2.1.2 RCurl_1.95-4.10 survival_2.42-3
## [79] abind_1.4-5 nnet_7.3-12 modelr_0.1.2
## [82] crayon_1.3.4 jomo_2.6-2 xgboost_0.71.2
## [85] utf8_1.1.4 rmarkdown_1.10 grid_3.5.0
## [88] readxl_1.1.0 data.table_1.11.4 ModelMetrics_1.1.0
## [91] digest_0.6.15 stats4_3.5.0 munsell_0.5.0
## [94] magic_1.5-8